Chapitre 7 Arbres et forêts aléatoires
Les arbres et les forêts aléatoires sont des méthodes prédictives s’appliquant autant aux variables réponses nominales que continues. Les approches ne sont pas particulièrement récentes. Les travaux de Kass (1980) sur l’algorithme CHAID ont essentiellement été réalisés dans le cadre de sa thèse dans les années 1970. Ceux de Breiman (2001) sur les forêts aléatoires datent de la fin du siècle dernier. C’est l’intérêt croissant du secteur de l’informatique pour les modèles prédictifs et l’augmentation fulgurante de la puissance de calcul qui ont rendu possible leur actuelle popularité.
7.1 Arbres de régression et de classification
7.1.1 Idée générale
L’idée générale des arbres de régression et de classification est de partir de l’ensemble des données d’entraînement et de les partitionner successivement sur la base de variables fortement discriminantes.
De façon très générale, les algorithmes fonctionnent ainsi:
- On part, à la racine, avec toutes les observations.
- On sélectionne une variable \(X_i\) et on subdivise le jeu de données en deux (ou plusieurs) noeuds sur la base de cette variable de sorte que la valeur de \(Y\) soit la plus homogène possible dans les deux noeuds.
- Pour chacun des deux noeuds créés, on répète l’étape 2.
- On poursuit ainsi jusqu’à l’atteinte d’un certain critère d’arrêt.
Le modèle créé est composé d’une longue suite de règles simples.
Illustrons le concept à l’aide d’un exemple simple dont les données sont présentées au tableau 7.1.
library(readxl)
don_achat <- read_excel("don/exemple_simple_arbre.xlsx")
don <- don_achat %>%
mutate_all(as.factor)%>%
slice(1:10)| age | revenu | etudiant | credit | achat |
|---|---|---|---|---|
| <=30 | eleve | non | bon | non |
| <=30 | eleve | non | excellent | non |
| 31-40 | eleve | non | bon | oui |
| >40 | moyen | non | bon | oui |
| >40 | faible | oui | bon | oui |
| >40 | faible | oui | excellent | non |
| 31-40 | faible | oui | excellent | oui |
| <=30 | moyen | non | bon | non |
| <=30 | faible | oui | bon | oui |
| >40 | moyen | oui | bon | oui |
La figure 7.1 illustre un exemple d’arbre pouvant être créé avec les données du tableau 7.1. Nous souhaitons prédire la variable achat, qui vaut oui (1) ou non (0). Le premier noeud, en haut, se nomme la racine et contient l’ensemble (100%) des observations. Dans ce noeud, 60% des individus ont acheté et 40% n’ont pas acheté. Ainsi, la valeur prédite à la racine de l’arbre serait «oui» et le taux d’erreur à la racine serait de 0,4 et l’exactitude serait de 0,6. Dans cet exemple, l’algorithme crée les deux premiers noeuds fils sur la base de la variable «âge». Toutes les observations pour lesquelles cette variable vaut «<=30» vont dans le noeud de gauche et toutes les observations pour lesquelles l’âge ne vaut pas «<=30» vont dans le noeud de droite.
Dans cet exemple, le noeud de droite est un noeud terminal (parfois appelé feuille), c’est-à-dire que cette branche de l’arbre cesse de croître (nous verrons dans les sections suivantes les critères pour qu’une branche cesse de croître). Les individus qui tombent dans ce noeud représentent 60% de l’échantillon d’entraînement. De ces six individus, 5 ont fait un achat et 1 seul n’en a pas fait. Les individus qui tombent dans ce noeud terminal seront donc prédits par ce modèle comme étant des acheteurs (\(\hat{y}=1\)). L’exactitude (sur l’échantillon d’entraînement) dans ce noeud sera de 0,83 et le taux d’erreur sera de 0,17.
Les individus du noeud de gauche représentent 40% de l’échantillon d’entraînement. La majorité (75%) d’entre eux n’ont pas fait d’achat. Ainsi, les individus tombant dans ce noeud seraient prédits comme n’étant pas des acheteurs (\(\hat{y}=0\)), avec un taux d’erreur de 0,25. Ce noeud n’est toutefois pas un noeud terminal; il est subdivisé à nouveau sur la base du revenu. Les individus de ce noeud dont le revenu est moyen ou élevé vont dans le noeud terminal de gauche et les individus dont le revenu est bas vont dans le noeud terminal de droite. Les deux nouveaux noeuds créés sont des noeuds purs, c’est-à-dire que tous les individus de ces noeuds prennent la même valeur de \(y\). Les 3 individus (30% de l’échantillon) du noeud de gauche n’ont pas acheté et l’individu du groupe de droite a acheté.
On peut ensuite utiliser le modèle pour prédire l’achat ou non d’un nouvel individu. Par exemple, s’il s’agit d’un individu de 30 ans ou moins au revenu bas, le modèle prédit qu’il achètera.
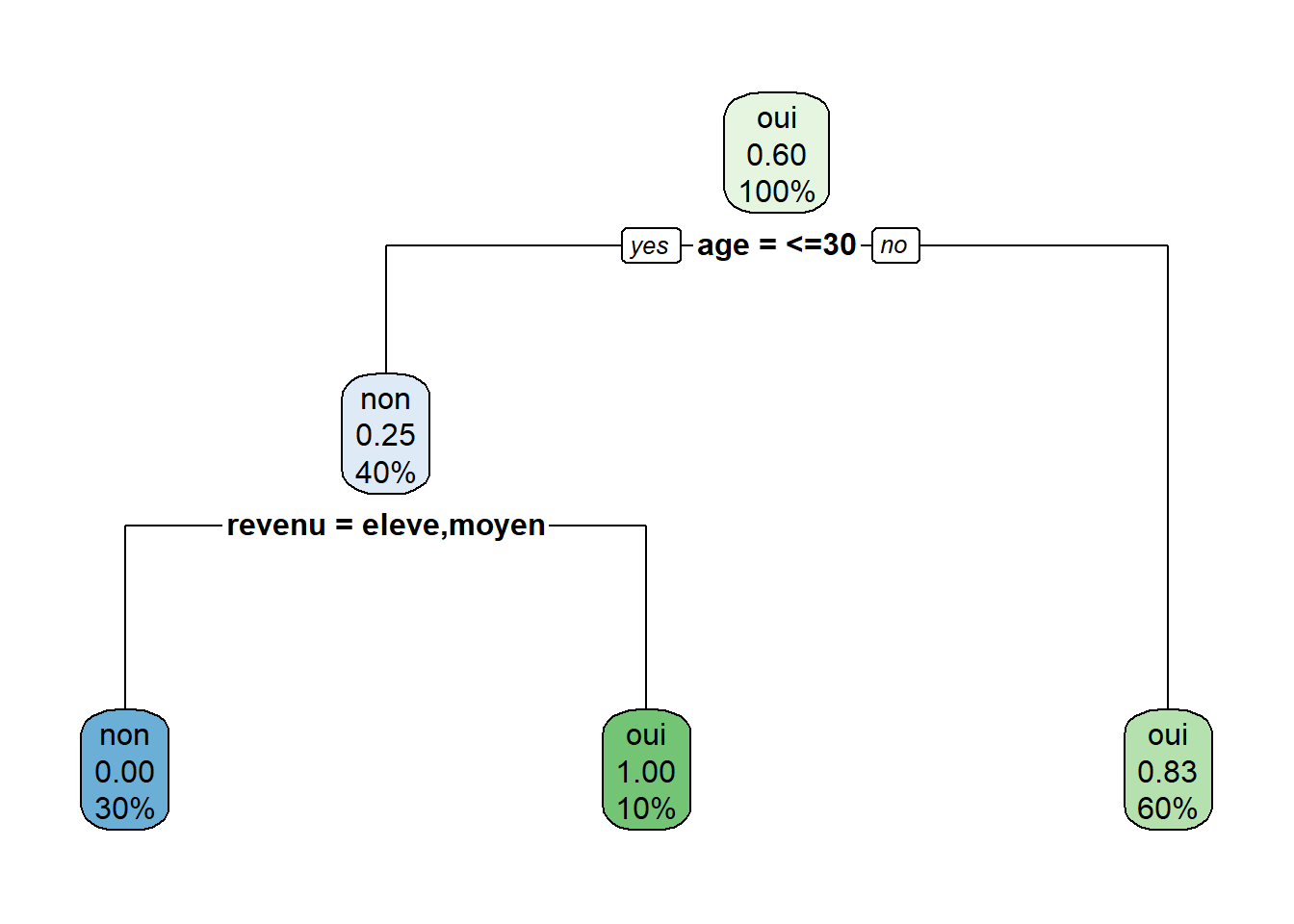
Figure 7.1: Exemple d’arbre simple
7.1.2 Mathématique
On peut voir les arbres de régression et de classification comme un partitionnement de l’espace en \(L\) régions \(S_1, S_2,...S_L\). Chaque région est associée à une valeur de la variable cible. Posons:
- \(L\), le nombre de régions
- \(n\), le nombre d’observations dans l’échantillon d’entraînement
- \(J\), le nombre de variables explicatives
- \(y_i\), la valeur de la variable cible pour l’observation \(i\), avec \(i\) allant de 1 à \(n\)
- \(\bf{x}_{i}\), le vecteur \((x_{i,1}, ..., x_{i,J})\) où \(x_{i,j}\) est la valeur de la variable \(j\) pour l’observation \(i\).
- \(k_l\), la valeur qu’on associa à \(y\) dans la région \(S_l\)
- \(\hat{y}_i\), la valeur prédite par le modèle pour l’observation \(i\) avec la fonction \(f(x_i)\)
Mathématiquement, le modèle s’écrit ainsi:
\[f(\mathbf{x})=\sum_{l=1}^L k_l \mathbf{1}(\mathbf{x}\in S_l)\]
où \(\mathbf{1}\) est la fonction indicatrice.9
Dans la construction du modèle, il faudra déterminer deux éléments:
- Quelle est la meilleure partition de l’espace? Autrement dit, quelles sont les meilleures régions \(S_l\) et combien de régions doit-on créer?
- Quelle est la valeur de \(k_l\) dans chacune des \(l\) régions?
L’objectif dans la construction du modèle est de trouver les \(S_l\) et les valeurs de \(k_l\) qui maximiseront un certain critère de performance. Par exemple, si la variable cible est continue, on pourrait vouloir choisir les \(S_l\) et les \(k_l\) de façon à minimiser \(E(\hat{y}_i-y_i)^2\).
La valeur de \(k_l\) est relativement simple à obtenir: dans le cas où \(y\) est nominal, on peut simplement prendre la classe la plus probable dans la région \(S_l\) et dans le cas où \(y\) est continue, on peut prendre la moyenne des valeurs de \(y\) dans la région \(S_l\).
La difficulté consiste à trouver la meilleure partition de l’espace. Idéalement, on essaierait toutes les partitions possibles et on choisirait celle qui offre la meilleure performance (selon le critère choisi). Cette approche est beaucoup trop exigeante en termes de calculs, mais on arrive généralement à une partition de l’espace intéressante (pas nécessairement la meilleure) en procédant avec des divisions successives, tel que présenté à la section 7.1.1.
7.1.3 Choix de la variable de séparation à chaque noeud
Les algorithmes diffèrent principalement sur la façon de choisir la variable de séparation à chaque noeud. Ces critères sont nombreux et les sections suivantes ne décrivent que les critères les plus populaires à l’heure actuelle.
7.1.3.1 Approche de type «CART»
Dans le cas binaire, le critère de sélection le plus populaire à l’heure actuelle est l’indice de Gini, qui se définit de la façon suivante:
\[Gini = \sum_{k=1}^Kp_k(1-p_k)=1-\sum_{k=1}^Kp_k^2\]
où \(p_k\) est la proportion d’observation appartenant à la classe \(k\) On le décrit comme un indice d’impureté d’un noeud. Dans le cas binaire (\(K=2\)), par exemple, l’indice de Gini sera maximal lorsqu’un noeud contient le même nombre d’observations dans les deux classes (\(p=0,5\)):
\[Gini = 1-(0.5^2+0,5^2)=0,5\]
Toujours dans le cas binaire (\(K=2\)), le critère sera minimal si toutes les observations du noeud prennent la même valeur:
\[Gini = 1-(1^2+0^2) = 0\]
Les algorithmes qui utilisent l’indice de Gini procèdent habituellement ainsi:
- On commence avec toutes les observations
- Pour chaque variable \(X_i\), on sépare les observations en deux selon les différentes valeurs que peut prendre \(X_i\).10
- On calcule l’indice de Gini des noeuds fils pour chaque séparation possible des \(X_i\)
- On choisit la séparation qui fait le plus diminuer de l’indice de Gini
- On répète les étapes 2 à 4 pour chaque noeud fils jusqu’à l’atteinte d’un critère d’arrêt.
Dans le cas où \(Y\) est continue, le critère le plus utilisé est l’erreur quadratique moyenne
\[EQM=E(\hat{y}_i-y_i)^2\],
calculée uniquement sur les observations du noeud que nous souhaitons séparer.
7.1.3.2 L’approche conditionnelle
L’approche conditionnelle consiste à choisir d’abord la variable de séparation, puis à choisir dans un deuxième temps la façon de combiner les valeurs de \(X_i\) pour obtenir la meilleure séparation possible.
Dans ce contexte, le réflexe naturel est de sélectionner la variable de séparation sur la base d’une mesure de dépendance entre \(Y\) et les \(X_i\). Si \(X\) et \(Y\) sont des variables nominales, on peut choisir la variable de séparation sur la base d’un test du \(\chi^2\). Autrement dit, on effectue un test d’indépendance du \(\chi^2\) entre \(Y\) et chacune des \(X_i\) et on choisit la variable pour laquelle la p-valeur est la plus faible. C’est ce que fait l’algorithme CHAID (Chi-squarred automatic interaction detection) proposé par Kass (1980).
Dans le cas de deux variables continues, on pourrait utiliser la corrélation entre \(X_i\) et \(Y\) et dans le cas d’un \(Y\) continu et de \(X_i\) nominales, nous pourrions utiliser le résultat du test de Fisher de l’analyse de variance.
7.1.4 Critères d’arrêt
L’obtention d’un noeud pur est un critère d’arrêt de croissance naturel, mais ce critère a de bonnes chances de mener à un surapprentissage. Pour cette raison, les algorithmes sont généralement construits de façon à s’arrêter sur la base d’autres critères d’arrêt. En voici quelques-uns:
L’effectif minimal dans chaque noeud terminal
Pour qu’un noeud soit séparé, les noeuds fils doivent avoir une taille minimale.
L’effectif minimal pour séparer un noeud
À partir d’une certaine valeur, un noeud ne peut plus être subdivisé et cette branche cesse de croître.
La hauteur (ou profondeur de l’arbre)
À partir d’une certaine hauteur, une branche cesse de croître.
La p-valeur (approches conditionnelles)
Les approches basées sur un test statistique offrent un avantage indéniable quant au critère d’arrêt en permettant de fixer ce dernier sur la base de la p-valeur. À partie d’un certain seuil, on considère que les variables sont indépendantes de \(Y\) et la branche cesse de croître.
La complexité (méthodes CART)
On peut jouer sur la croissance de l’arbre en ajoutant au critère de sélection de la variable un paramètre de pénalisation pour la complexité de l’arbre. Si, par exemple, \(Y\) est continue, le critère du coût de complexité d’un arbre T est
\[C_\alpha(T)=\sum_{w=1}^{|T|}Q_w+\alpha |T|\]
où
- \(|T|\) est le nombre de noeuds terminaux dans l’arbre T
- \(Q_w\) est l’erreur quadratique (\(\sum(y_i-\hat{y}_i)^2\)) dans le noeud \(w\)
- \(\alpha\) est le paramètre de pénalisation
On voit que si le paramètre \(\alpha\) est nul, il n’y a aucune pénalisation pour la complexité de l’arbre. Plus ce paramètre augmente, plus on pénalise pour la complexité.
7.1.5 En pratique
Les deux principales librairies en R pour créer des arbres sont les rpart et party. La librairie rpart utilise une approche de type «CART» alors que la librairie party utilise une approche conditionnelle.
Voici un exemple pour obtenir un arbre de type CART avec les données du tableau 7.1.
library(rpart)
library(rpart.plot)
# Hyperparamètres
hp <- rpart.control(minsplit = 2, #L'effectif minimal pour séparer un noeud
minbucket = 1, # L'effectif minimal dans chaque noeud terminal
maxdepth = 30, # Hauteur (profondeur) maximale de l'arbre
cp = 0 # Paramètre de pénalisation pour la complexité
)
# Construction de l'arbre
arbre_rpart <- rpart(achat~., # Y~X
don, # Données
control = hp # Hyperparamètres
)
# Afficher l'arbre
arbre_rpartFALSE n= 10
FALSE
FALSE node), split, n, loss, yval, (yprob)
FALSE * denotes terminal node
FALSE
FALSE 1) root 10 4 oui (0.4000000 0.6000000)
FALSE 2) age=<=30 4 1 non (0.7500000 0.2500000)
FALSE 4) revenu=eleve,moyen 3 0 non (1.0000000 0.0000000) *
FALSE 5) revenu=faible 1 0 oui (0.0000000 1.0000000) *
FALSE 3) age=>40,31-40 6 1 oui (0.1666667 0.8333333)
FALSE 6) credit=excellent 2 1 non (0.5000000 0.5000000)
FALSE 12) age=>40 1 0 non (1.0000000 0.0000000) *
FALSE 13) age=31-40 1 0 oui (0.0000000 1.0000000) *
FALSE 7) credit=bon 4 0 oui (0.0000000 1.0000000) *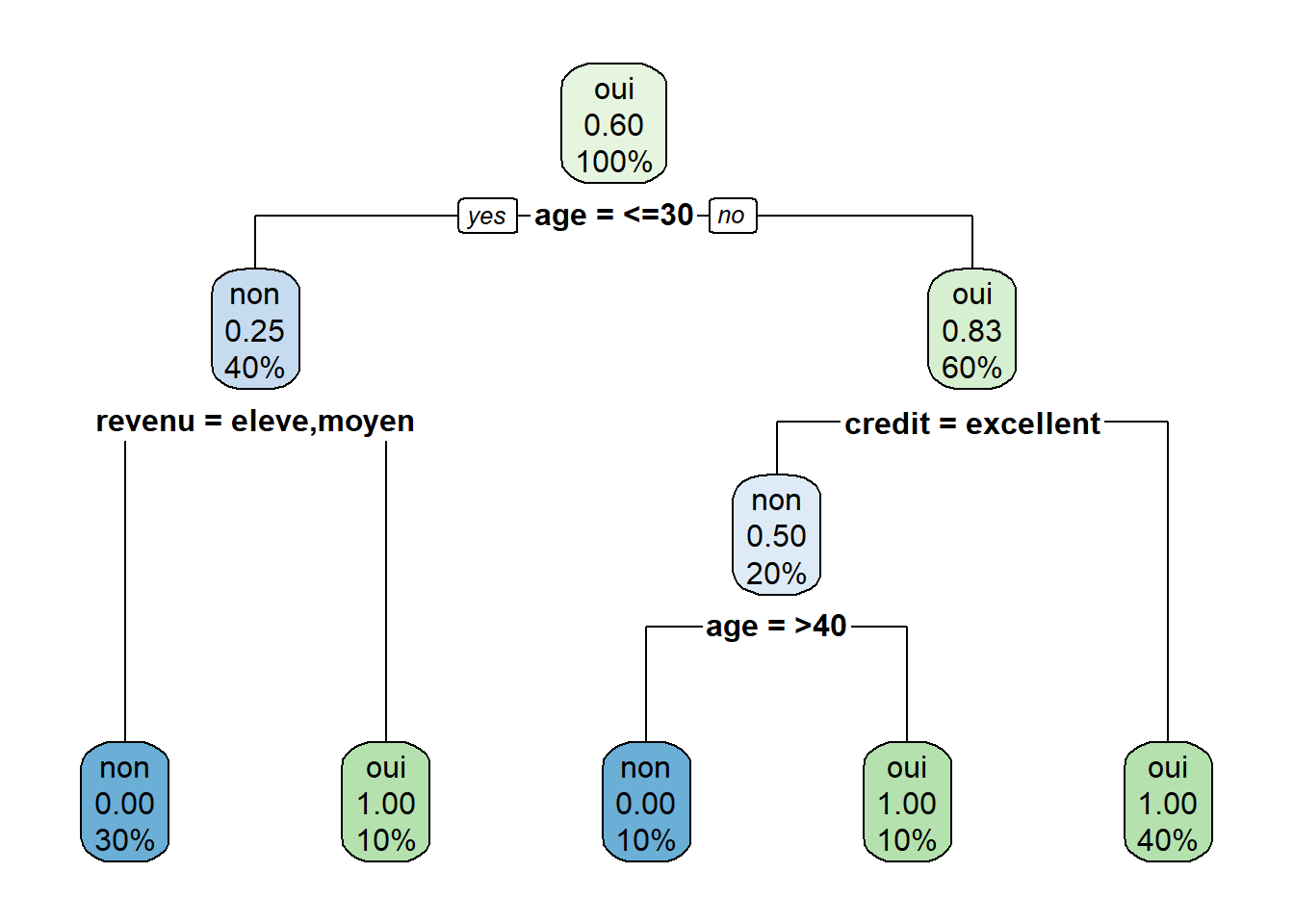
# Faire une prédiction avec l'arbre
hat_y <- predict(arbre_rpart, # Le modèle créé par rpart
don, # Le jeu de données que l'on souhaite prédire
type = 'class' # Le type de prédiction que l'on souhaite obtenir (une classe ou une probabilité)
)La librairie visNetwork (Almende B.V., Thieurmel, and Robert (2019)) permet une visualisation interactive particulièrement intéressante des arbres. Vous trouverez un excellent tutoriel ici: http://datastorm-open.github.io/visNetwork/.
Voici un exemple pour construire un arbre conditionnel avec les données du tableau 7.1.
# Charger la librairie
library(party)
# Choisir les hyperparamètres
hp <- ctree_control(minsplit = 2, #L'effectif minimal pour séparer un noeud
minbucket = 1, # L'effectif minimal dans chaque noeud terminal
maxdepth = 30, # Hauteur (profondeur) maximale de l'arbre
mincriterion = 0.3) # 1-p-valeur à partir de laquelle on souhaite cesser la croissance)
# Construire l'arbre
arbre_ctree <- ctree(achat~., don,control = hp)
# Afficher l'arbre
arbre_ctreeFALSE
FALSE Conditional inference tree with 4 terminal nodes
FALSE
FALSE Response: achat
FALSE Inputs: age, revenu, etudiant, credit
FALSE Number of observations: 10
FALSE
FALSE 1) age == {<=30}; criterion = 0.441, statistic = 3.375
FALSE 2) revenu == {eleve}; criterion = 0.364, statistic = 3
FALSE 3)* weights = 2
FALSE 2) revenu == {faible, moyen}
FALSE 4)* weights = 2
FALSE 1) age == {>40, 31-40}
FALSE 5) credit == {bon}; criterion = 0.504, statistic = 2
FALSE 6)* weights = 4
FALSE 5) credit == {excellent}
FALSE 7)* weights = 2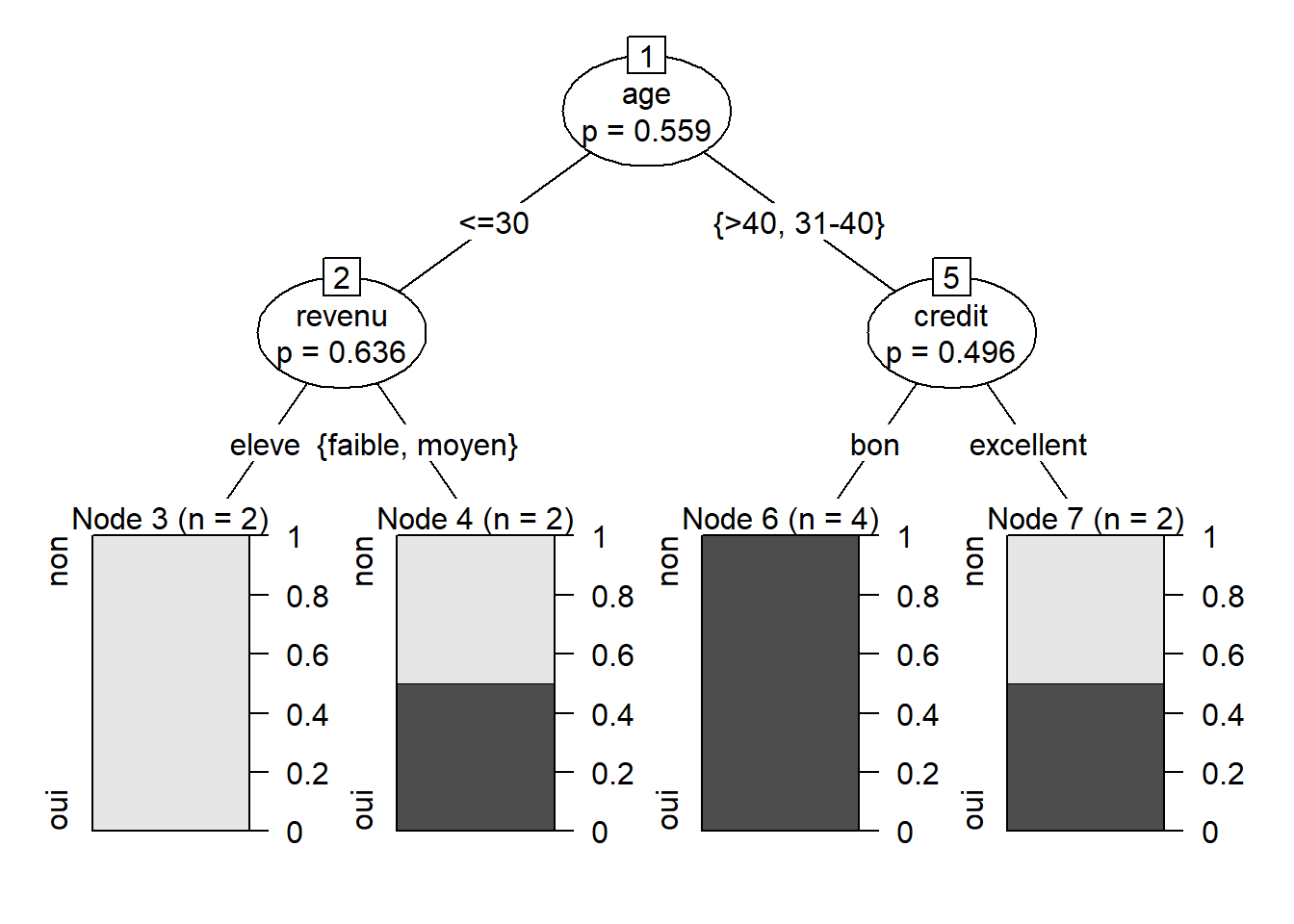
7.1.6 Avantages et inconvénients des arbres
Les principaux avantages des arbres de régression sont:
- Aucune hypothèse a priori n’est faite sur la distribution des données
- Robuste aux données extrêmes
- Facile à interpréter si l’arbre est petit
- Tient implicitement compte des interactions possibles entre les variables
- Sélectionne implicitement les variables importantes
- Permet d’obtenir un modèle non linéaire
Les inconvénients sont les suivants:
- L’approche n’est pas particulièrement performante en termes de prédiction
- Les risques de surapprentissage sont élevés
- Nous ne sommes pas certains d’atteindre la meilleure partition
- Peut être instable dans les résultats qu’elle produit
- Les algorithmes de construction des arbres nécessitent un temps d’exécution élevé
7.2 Les méthodes d’ensemble
Il arrive qu’un même algorithme appliqué à un ensemble de données d’apprentissage légèrement différent produise un modèle très différent.
Un algorithme pour construire un modèle de prédiction est dit instable si de petits changements dans les données d’apprentissage engendrent de grands changements dans le modèle et possiblement aussi dans les valeurs prédites par ce dernier.
Une moyenne de plusieurs mesures est généralement plus précise qu’une mesure individuelle. Une moyenne est aussi beaucoup plus stable qu’une seule mesure: si différents échantillons sont recueillis d’une même population, leurs moyennes seront beaucoup plus semblables que les valeurs individuelles dans un échantillon.
Un phénomène semblable se produit pour les modèles de prédiction ou de classification: une moyenne de valeurs prédites par différents modèles est souvent plus précise et plus stable que la valeur prédite à l’aide d’un seul modèle.
Une méthode d’ensemble est un ensemble de modèles dont les prédictions sont combinées d’une certaine manière afin d’obtenir une prédiction plus stable.
Voici différentes façons de combiner les données:
- Variable cible continue:
- moyenne des valeurs prédites par chaque modèle.
- Variable cible de type nominale:
- moyenne des probabilités a prédites de chaque modèle pour chaque classe de la variable cible
- classification dans la classe de la variable cible pour laquelle le plus grand nombre de modèles classifie l’observation (vote le plus populaire!).
7.2.1 Le bagging
Le terme bagging vient de la concaténation des termes bootstrap aggregating. Le concept est assez général et pourrait s’appliquer à différents types de modèles. Lorsqu’appliqué aux arbres, il consiste à faire plusieurs arbres à partir de différents sous-échantillons de l’ensemble d’entraînement et à agréger les résultats de tous les arbres.
On procède ainsi:
- On sélectionne (généralement avec remise) un échantillon des données de taille \(c\)
- On construit un arbre \(b\)
- On calcule une prévision pour chaque observation (\(\hat{y}_i^{(b)}\))
- On répète les étapes 1 à 3 B fois (\(b = (1,2...,B)\))
- On agrège les valeurs des B arbres (par exemple, on peut prendre \(\hat{y}_i= \frac{1}{B}\sum_{b=1}^{B}\hat{y}_i^{(b)}\))
Le bagging est beaucoup plus stable et plus performant en termes de prévisions qu’un arbre individuel. Il offre en outre l’avantage d’avoir, pour chaque arbre, une partie de l’échantillon qui n’est pas utilisée et qui peut être utilisée pour évaluer la performance de chaque arbre individuel (en anglais, on parle d’échantillon OOB pour out of bag).
Les inconvénients par rapport aux arbres sont d’une part qu’ils sont plus longs à calculer (typiquement, on fait environ 500 arbres) et d’autre part, qu’ils impliquent la sélection de deux hyperparamètres supplémentaires (la taille de l’échantillon \(c\) et le nombre d’arbres \(B\)).
7.2.2 Le boosting
Comme le bagging, le boosting construit plusieurs arbres et agrège les résultats. À la différence du bagging, le boosting procède de façon séquentielle en modifiant à chaque itération le poids des observations.
On procède ainsi:
On fixe des poids d’échantillonnage égaux pour chaque observation (\(w_i^{(1)} = \frac{1}{N}\))
On sélectionne un échantillon aléatoire de taille \(c\) en utilisant les poids calculés en 1 ou à l’itération précédente.
On crée un arbre et on fait une prédiction pour chaque observation
On modifie les poids de façon à donner plus de poids aux observations mal classifiées
\[w_i^{(b+1)} = \frac{1+(\hat{y}_i^{(b)}-y_i)^4}{\sum_{j=1}^{N}(1+(\hat{y}_i^{(b)}-y_i)^4)}\]
On répète les étapes 2 à 4 \(B\) fois
On agrège les résultats. Dans certains cas, le poids des arbres dans le résultat final peut être ajusté selon les performances du modèle.
7.2.3 Les forêts aléatoires
On pousse la perturbation un peu plus loin: à chaque noeud de l’arbre, on sélectionne la variable parmi un échantillon des variables disponibles.
On procède ainsi:
On sélectionne (généralement avec remise) un échantillon des données de taille \(c\)
On construit un arbre \(b\) de la façon suivante:
- On part, à la racine, avec toutes les observations de l’échantillon sélectionné en 1.
- On sélectionne \(d\) variables parmi l’ensemble des variables disponibles.
- Pour chacune des \(d\) variables sélectionnées en ii, on calcule l’indice de Gini (ou un autre critère) pour chacune des divisions (ou combinaisons de modalités) possibles.
- On choisit la variable et la division qui fait le plus descendre l’indice de Gini et on crée deux nouveaux noeuds sur cette base.
- Pour chacun des deux noeuds créés, on répète les étapes ii à iv jusqu’à l’atteinte d’un certain critère d’arrêt.
On calcule une prévision pour chaque observation (\(\hat{y}_i^{(b)}\))
On répète les étapes 1 à 3 B fois (\(b = (1,2...,B)\))
On agrège les valeurs des B arbres (par exemple, on peut prendre \(\hat{y}_i= \frac{\sum_{b=1}^{B}\hat{y}_i^{(b)}}{B}\))
Les forêts aléatoires sont plus robustes que le bagging car le fait de choisir un échantillon des variables à chaque noeud entraîne une décorrélation des arbres. Ils sont donc en général plus performants tout en requérant moins de temps de calcul que le bagging.
La construction d’une forêt aléatoire implique cependant la sélection d’un hyperparamètre de plus: \(d\), le nombre d’arbres que l’on sélectionne à chaque noeud.
Il est à noter que Breiman (2001) a démontré la convergence presque sûre des forêts aléatoires: plus le nombre d’arbres augmente, plus on se dirige vers le meilleur modèle.
Références
Almende B.V., Benoit Thieurmel, and Titouan Robert. 2019. VisNetwork: Network Visualization Using Vis.js Library. https://CRAN.R-project.org/package=visNetwork.
Breiman, Leo. 2001. “Random Forests.” Machine Learning 45 (1): 5–32.
Kass, Gordon V. 1980. “An Exploratory Technique for Investigating Large Quantities of Categorical Data.” Applied Statistics, 119–27.