Chapitre 4 Analyse factorielle des correspondances
Au chapitre précédent nous avons vu que l’analyse en composante principale (ACP) pouvait permettre de visualiser, de découvrir une structure ou réduire la dimension d’ensembles de plusieurs variables continues. Dans ce chapitre, nous verrons comment il est aussi possible de le faire lorsque les variables sont catégorielles, par exemple des variables rapportées dans des tableaux de contingences ou des réponses à des questionnaires à choix multiples.
L’analyse des correspondances est une méthode d’origine française (vous trouverez beaucoup de documentation en français!). Elle permet de représenter graphiquement des tableaux de fréquences. On verra deux familles de méthodes:
- analyse des correspondances binaires: pour des tableaux de fréquences croisant deux variables;
- analyse des correspondances multiples: pour des tableaux faisant intervenir trois variables ou plus.
L’analyse des correspondances binaires sera illustrée à partir de l’exemple suivant.
Exemple 4.1 On s’intéresse à la relation entre la couleur des yeux et la couleur des cheveux de 592 sujets féminins. Les données sont résumées dans le tableau 4.1. Les données s’inspirent de l’article de Snee (1974)
Il serait intéressant de voir si des relations existent entre les modalités des deux variables, aussi de faire une représentation visuelle des données qui fait ressortir les associations les plus fortes.# Tableau de fréquence cheveux x yeux
kij <- data.frame(Chatains = c(119,54,29,84), Roux = c(26,14,14,17), Blonds = c(7,10,16,94),
row.names = c('Marrons','Noisette','Verts','Bleus'))| Chatains | Roux | Blonds | |
|---|---|---|---|
| Marrons | 119 | 26 | 7 |
| Noisette | 54 | 14 | 10 |
| Verts | 29 | 14 | 16 |
| Bleus | 84 | 17 | 94 |
Dans l’exemple 4.1, nous voyons que les personnes aux yeux bleus ont tendance à être plus souvent blondes et que les personnes aux cheveux châtains sont plus susceptibles d’avoir les yeux bruns. Nous sommes en mesure de le constater d’une part parce que l’idée est assez intuitive et d’autre part parce que le tableau est de très petite dimension. Expliquer ou décrire le lien entre deux variables qualitatives est beaucoup plus difficile lorsque le nombre de modalités est plus grand ou lorsque le projet est réellement exploratoire (c’est-à-dire que nous n’avons pas d’idée a priori du lien entre les variables).
Dans l’analyse des correspondances, nous exploiterons la notion de distance entre les lignes et de distance entre les colonnes pour illustrer l’ensemble des modalités sur un même graphique afin de visualiser des relations entre des modalités. On cherchera à représenter visuellement les modalités des deux variables dans le même plan de façon à ce que deux modalités liées positivement (deux modalités pour lesquelles l’effectif est plus grand que ce à quoi on se serait attendu sous l’indépendance) soient près l’une de l’autre.
4.1 Concepts et notation
L’analyse des correspondances binaires se fait lorsque l’on a deux variables catégorielles \(X\) (avec \(n\) modalités) et \(Y\) (avec \(p\) modalités).
4.1.1 Fréquences et fréquences relatives
Soit \(\bf{K} = k_{i,j}\), le tableau de fréquence où \((k_{i,j})\) est le nombre d’individus appartenant à la catégorie \(i\) de \(X\) et à la catégorie \(j\) de \(Y\). Le tableau 4.1 est un tableau de fréquence. On utilise parfois le terme «tableau de contingence».
Comme les fréquences sont proportionnelles à la taille de l’échantillon, il est souvent plus pertinent de travailler avec le tableau de fréquences relatives,
Il s’agit du tableau \[{\bf{F}} = (f_{ij}),\] dans lequel \[f_{ij} = \frac{k_{ij}}{k_{\bullet \bullet}} = \frac{k_{ij}}{\sum_{\ell=1}^n \sum_{m=1}^p k_{\ell m}} \, . \]
Dans l’exemple 4.1, on obtient le tableau des fréquences relatives suivant:
# Calculer le nombre total d'observations
kpp <- sum(kij)
# Calculer le tableau des fréquences relatives
fij <- kij / kpp| Chatains | Roux | Blonds | |
|---|---|---|---|
| Marrons | 0.25 | 0.05 | 0.01 |
| Noisette | 0.11 | 0.03 | 0.02 |
| Verts | 0.06 | 0.03 | 0.03 |
| Bleus | 0.17 | 0.04 | 0.19 |
4.1.2 Marges
Nous aurons aussi besoin de la somme des colonnes pour chaque ligne et de la somme des lignes pour chaque colonne, ce qu’on appelle les marges du tableau:
\[ \begin{align*} f_{i \bullet} &= \sum_{j=1}^p f_{ij} = k_{i \bullet}/k_{\bullet \bullet} \, , \quad 1 \le i \le n\,;\\ f_{\bullet j} &= \sum_{i=1}^n f_{ij} = k_{\bullet j}/k_{\bullet \bullet} , \quad 1 \le j \le p. \\ \end{align*} \]
On ajoute facilement les marges à un tableau avec la fonction addmargins.
# Conversion du tableau de fréquence en matrice
# (En R, le calcul matriciel se fait sur des matrices)
fij_mat <- as.matrix(fij)
# Ajout des marges au tableau de fréquences relatives
fij_marge <- as.data.frame(addmargins(fij_mat))| Chatains | Roux | Blonds | Sum | |
|---|---|---|---|---|
| Marrons | 0.25 | 0.05 | 0.01 | 0.31 |
| Noisette | 0.11 | 0.03 | 0.02 | 0.16 |
| Verts | 0.06 | 0.03 | 0.03 | 0.12 |
| Bleus | 0.17 | 0.04 | 0.19 | 0.40 |
| Sum | 0.59 | 0.15 | 0.26 | 1.00 |
4.1.3 Profils
Profils lignes
Le profil ligne est \[\begin{equation}\label{eq:profl} L_i = \left( \frac{k_{i1}}{k_{i \bullet}} \, , \ldots , \frac{k_{ip}}{k_{i\bullet}} \right) = \left( \frac{f_{i1}}{f_{i \bullet}} \, , \ldots , \frac{f_{ip}}{f_{i\bullet}} \right), \end{equation}\]
On l’obtient en divisant chaque valeur par le total de la ligne correspondant:
| Chatains | Roux | Blonds | |
|---|---|---|---|
| Marrons | 0.78 | 0.17 | 0.05 |
| Noisette | 0.69 | 0.18 | 0.13 |
| Verts | 0.49 | 0.24 | 0.27 |
| Bleus | 0.43 | 0.09 | 0.48 |
Interprétons la deuxième ligne, première colonne: 69 % des personnes aux yeux noisettes ont les cheveux châtains.
En termes matriciels, on posera \(D_n = diag(f_{i\bullet})\) de sorte que
\[L = D_n^{-1}F\].
On obtiendra donc le même résultat avec:
# Calcul des profils lignes (version matricielle)
Dn <- diag(margin.table(fij_mat,1))
L <- solve(Dn) %*% fij_matOn peut ensuite définir le profil-ligne moyen
\[\begin{equation} \left( \sum_{i=1}^n f_{i \bullet} \; \frac{f_{i1}}{f_{i \bullet}} \, , \ldots , \sum_{i=1}^n f_{i \bullet} \; \frac{f_{ip}}{f_{i \bullet}} \right) = \left( f_{\bullet 1}, \ldots , f_{\bullet p} \right). \end{equation} \]
Qu’on obtient simplement en sommant les colonnes de notre tableau de fréquence:
| Chatains | Roux | Blonds |
|---|---|---|
| 0.59 | 0.15 | 0.26 |
La première valeur s’interprète simplement de la façon suivante: 59 % des personnes ont les cheveux chatains.
Remarquez que si la couleur des cheveux et des yeux étaient des variables indépendantes, les profils-lignes présentés au tableau 4.4 seraient tous similaires au profil ligne moyen du tableau 4.5. Ainsi, la dépendance entre les variables sera fonction de la ressemblance (ou de la distance) entre les lignes.
Profils colonne
Le profil colonne, pour la colonne \(j\), s’écrit
\[ \begin{equation} C_j = \left( \frac{k_{1j}}{k_{\bullet j}} \, , \ldots , \frac{k_{nj}}{k_{\bullet j}} \right) = \left( \frac{f_{1j}}{f_{\bullet j}} \, , \ldots , \frac{f_{nj}}{f_{\bullet j}} \right). \end{equation} \]
On l’obtient en divisant chaque valeur par le total de la colonne correspondant. Comme pour les profils ligne, on peut l’exprimer et le calculer en termes matriciels en posant \(D_p = diag(f_{\bullet j})\), de sorte que
\[C = D_p^{-1}F^\top\]
# Calcul des profils colonnes (matriciel)
Dp <- diag(margin.table(fij_mat,2))
C <- solve(Dp) %*% t(fij_mat)
rownames(C) <- colnames(fij_mat)| Marrons | Noisette | Verts | Bleus | |
|---|---|---|---|---|
| Chatains | 0.42 | 0.19 | 0.10 | 0.29 |
| Roux | 0.37 | 0.20 | 0.20 | 0.24 |
| Blonds | 0.06 | 0.08 | 0.13 | 0.74 |
Comme on l’a fait avec les profils-lignes, on peut ensuite définir le profil-colonne moyen:
\[ \begin{equation} \left( \sum_{j=1}^p f_{\bullet j} \; \frac{f_{1j}}{f_{\bullet j}} \, , \ldots , \sum_{j=1}^p f_{\bullet j} \; \frac{f_{nj}}{f_{\bullet j}} \right) = \left( f_{1 \bullet} , \ldots , f_{n \bullet} \right). \end{equation} \]
Qu’on obtient simplement en sommant les lignes de notre tableau de fréquence:
| Marrons | Noisette | Verts | Bleus |
|---|---|---|---|
| 0.31 | 0.16 | 0.12 | 0.4 |
La première valeur s’interprète simplement de la façon suivante: 31 % des personnes ont les yeux bruns.
Comme c’était le cas avec les profils-ligne, si la couleur des cheveux et des yeux étaient des variables indépendantes, les profils colonnes présentés au tableau 4.6 seraient tous similaires au profil colonne moyen du tableau 4.7. Ainsi, la dépendance entre les variables sera fonction de la ressemblance (ou de la distance) entre les colonnes.
4.1.4 Distances entre les profils
On peut mesurer la distance entre deux profils-lignes par \[d^2 (i,i^\prime) = \sum_{j=1}^p \left( \frac{f_{ij}}{f_{i \bullet}} - \frac{f_{i^\prime j}}{f_{i^\prime \bullet}} \right)^2. \] Cependant, cette distance ne tient pas compte de l’importance de chaque colonne. Un choix plus judicieux consiste à prendre la distance du khi deux, qui tient compte de l’importance de chaque colonne.
\[ \begin{equation} d^2 (i,i^\prime) = \sum_{j=1}^p \frac{1}{f_{\bullet j}} \, \left( \frac{f_{ij}}{f_{i \bullet}} - \frac{f_{i^\prime j}}{f_{i^\prime \bullet}} \right)^2. \end{equation} \]
\[ \begin{equation} d^2 (1,2) = \frac{1}{0.591} \left(\frac{0.246}{0.314} - \frac{0.112}{0.161} \right)^2 + \frac{1}{0.147} \left(\frac{0.054}{0.314} - \frac{0.029}{0.161} \right)^2 + \frac{1}{0.262} \left(\frac{0.014}{0.314} - \frac{0.021}{0.161} \right)^2 \end{equation} \]
Utilisons la notation \(x\) pour faire référence au vecteur des distances entre deux lignes \(L_{11} - L{21}\) ou entre deux colonnes \(C_{11}-C_{12}\). En adoptant la notation matricielle, on obtient que la distance carrée du khi deux est de la forme
\[x^\top D_p^{-1} x = \sum_{j=1}^p \frac{x_j^2}{f_{\bullet j}}\] pour un point-ligne \(x \in \mathbb{R}^p\) et de la forme
\[x^\top D_n^{-1} x = \sum_{i=1}^n \frac{x_i^2}{f_{i \bullet}}\] pour un point-colonne \(x \in \mathbb{R}^n\).
Voici un exemple de calcul en R pour la distance entre les lignes 1 et 2, puis entre les lignes 1 et 4:
# Distance du chi2 entre les lignes 1 et 2
x12 <- as.matrix(L[1,] - L[2,])
d_euclidienne_ligne_12 <- t(x12) %*% x12
d_chi2_ligne_12 <- t(x12) %*% as.matrix(solve(Dp)) %*% (x12)
# Distance du chi2 entre les lignes 1 et 4
x14 <- as.matrix(L[1,] - L[4,])
d_euclidienne_ligne_14 <- t(x14) %*% diag(3) %*% x14
d_chi2_ligne_14 <- t(x14) %*% solve(Dp) %*% x14La distance euclidienne entre les lignes 1 (yeux marrons) et 2 (yeux noisettes) est de 0.02. La distance du \(\chi^2\) est de 0.04. La distance euclidienne entre les lignes 1 (yeux marrons) et 4 (yeux bleus) est de 0.32; la distance du \(\chi^2\) est de 0.98. On peut interpréter ces valeurs ainsi: les personnes aux yeux marron ont des cheveux qui ressemblent davantage à ceux des personnes aux yeux verts qu’à ceux aux yeux bleus.
Notez que les deux distances (euclidienne et du \(\chi^2\)) nous mènent à la même conclusion. Alors pourquoi privilégier la distance du \(\chi^2\) ? Voici les deux avantages de la distance du \(\chi^2\):
- elle garantit l’équivalence distributionnelle;
- elle garantit relation quasi barycentrique2 entre les deux nuages de points \[L_1, \ldots , L_n \in \mathbb{R}^p \quad C_1, \ldots , C_p \in \mathbb{R}^n.\]
Quelques constats supplémentaires…
4.1.5 Indépendance
Les fréquences relatives estiment des probabilités. On dit que deux variables aléatoires \(X\) et \(Y\) sont indépendantes quand \(P[X=x,Y=y]=P[X=x]P[Y=y]\) pour toutes les paires \((x,y)\). Dans le cas d’un tableau de fréquences croisant deux variables, sous l’hypothèse d’indépendance les fréquences relatives devraient être telles qu’on ne s’éloigne pas trop de la relation \[\quad \forall_{i, j} \quad f^{(ind)}_{ij} = f_{i \bullet} f_{\bullet j}.\] Dans l’exemple 4.1, si la couleur des cheveux et des yeux étaient indépendantes, le tableau des fréquences relatives 4.2 devrait ressembler à
# Calcul des fréquences attendues sous l'indépendance
fij_ind <- margin.table(fij_mat,1) %*% t(margin.table(fij_mat,2))| Chatains | Roux | Blonds | |
|---|---|---|---|
| Marrons | 0.19 | 0.05 | 0.08 |
| Noisette | 0.10 | 0.02 | 0.04 |
| Verts | 0.07 | 0.02 | 0.03 |
| Bleus | 0.24 | 0.06 | 0.11 |
Cette hypothèse est souvent testée à l’aide d’un test du \(\chi^2\) En effet, on sait que sous l’hypothèse d’indépendance,
\[ \begin{align*} Z^2 &= \sum_{i=1}^n \sum_{j=1}^p \frac{[k_{ij} - E(k_{ij})]^2 }{E(k_{ij})}\\[12pt] & = \sum_{i=1}^n \sum_{j=1}^p \frac{\left( k_{ij} - \frac{k_{i\bullet} k_{\bullet j}}{k_{\bullet \bullet}} \right)^2 }{ \left(\frac{k_{i \bullet} k_{\bullet j}}{k_{\bullet \bullet}} \right)}\\ & = k_{\bullet \bullet} \sum_{i=1}^n \sum_{j=1}^p \frac{\left( f_{ij} - f^{(ind)}_{ij}\right)^2}{f^{(ind)}_{ij}}\\ &\approx \chi^2_{(n-1)(p-1)}. \end{align*} \]
Dans l’exemple 4.1, on obtient:
# Calcul de la statistique du test
Z2 <- kpp*sum((fij-fij_ind)^2/fij_ind)
# Calcul des degrés de liberté
n <- ncol(kij)
p <- nrow(kij)
ddl <- (n-1)*(p-1)La valeur de la statistique de test est \(Z^2 =97.8218604\) et le nombre de degrés de liberté est de \((n-1)(p-1) = 6\). Sous l’indépendance, cette statistique suit une distribution du \(\chi^2\) avec 6 degrés de liberté.
FALSE [1] 7.141485e-19Puisque la p-valeur du test est inférieure à 0,05, on peut conclure que la couleur des yeux et des cheveux ne sont pas indépendantes.
Ce test nous permet de supposer qu’il y a un lien entre les deux variables, mais il ne nous permet pas d’expliquer ou de décrire davantage ce lien.
4.2 Mathématique de l’analyse des correspondances binaires
en réalisant une analyse des correspondances, on cherche à représenter simultanément les profils lignes appartenant à \(\mathbb{R}^p\) et les profils colonnes appartenant à \(\mathbb{R}^n\) d’un tableau de fréquences. Comme cette représentation est faite dans le plan cartésien, elle sera obtenue à l’aide d’une double analyse en composantes principales.
Les deux analyses en composantes principales ne sont pas réalisées directement sur les variables, mais plutôt sur les profils lignes (analyse directe) et les profils colonnes (analyse duale) présentés dans la section 4.1.4. De plus, l’analyse des correspondances binaires intègre la notion de poids des colonnes (ou des lignes) et de distance du \(\chi^2\). Le tableau 4.9 permet de comparer sommairement l’analyse en composantes principales avec l’analyse des correspondances.
| ACP | AFC (analyse directe) | AFC (analyse duale) | |
|---|---|---|---|
| Données | \(X\) | \(D_n^{-1}F\) | \(D_p^{-1}F^\top\) |
| Poids | \(I\) | \(D_n^{-1}\) | \(D_p^{-1}\) |
| Distances | \(I\) | \(D_p^{-1}\) | \(D_n^{-1}\) |
| Projections | \(Xu\) | \((D_n^{-1}F)D_p^{-1}u\) | \((D_p^{-1}F^\top)D_n^{-1}v\) |
| À maximiser | \(u^\top X^\top X u\) | \((u^\top D_p^{-1}F^\top D_n^{-1})D_n(D_n^{-1}FD_p^{-1}u)\) | \((v^\top D_n^{-1}F D_p^{-1})D_p(D_p^{-1}F^\top D_n^{-1}v)\) |
| Contrainte | \(u^\top u=1\) | \(u^\top D_p^{-1} u=1\) | \(u^\top D_n^{-1} u=1\) |
4.2.1 Analyse directe (lignes)
L’analyse directe est effectuée sur les profils lignes. Les lignes de \(L = D_n^{-1}F\) sont des éléments de \(\mathbb{R}^p\). On cherche à les représenter dans cet espace muni de la fonction de distance \(x^\top D_p^{-1} x.\)
Dans l’analyse directe, on cherche le vecteur \(u \in \mathbb{R}^p\) tel que \[(u^\top D_p^{-1}F^\top D_n^{-1})D_n(D_n^{-1}FD_p^{-1}u)\] soit maximal, sachant que \(u^\top D_p^{-1}u = 1\).
On trouve la solution en utilisant la proposition A.3 (avec \(A = (D_p^{-1}F^\top D_n^{-1} FD_p^{-1})\) et \(M = D_p^{-1}\)). La solution est donnée par le vecteur propre principal de \[D_p (D_p^{-1}F^\top D_n^{-1} FD_p^{-1}) = F^\top D_n^{-1}FD_p^{-1}\equiv S.\] Calculons \(S\)
# Matrice dont on cherche les vecteurs propres dans l'analyse directe
S <- t(fij_mat) %*% solve(Dn) %*% fij_mat %*% solve(Dp)Et calculons ses valeurs propres et vecteurs propres:
| 1 | 0.19 | 0.01 |
| -0.89 | -0.62 | 0.71 |
| -0.22 | -0.16 | -0.70 |
| -0.40 | 0.77 | -0.01 |
Le \(j^{\rm e}\) facteur de l’analyse directe est défini par \[\varphi_j = D_p^{-1}u_j, \quad 1 \le j \le p.\]
Les projections des profils des lignes (leurs coordonnées) sur le \(j^{\rm e}\) vecteur propre \(u_j\) sont les composantes du vecteur \(D_n^{-1}F \varphi_j\).
coord_ligne2 <- solve(Dn) %*% fij_mat %*% varphi_j2
coord_ligne3 <- solve(Dn) %*% fij_mat %*% varphi_j3On peut représenter les profils-lignes sur les deux dimensions de l’analyse des correspondances.
dat <- data.frame(dim1 = coord_ligne2, dim2 = coord_ligne3)
ggplot()+
geom_label(aes(dim1,dim2, label = c('Marrons','Noisettes','Verts','Bleus')), dat)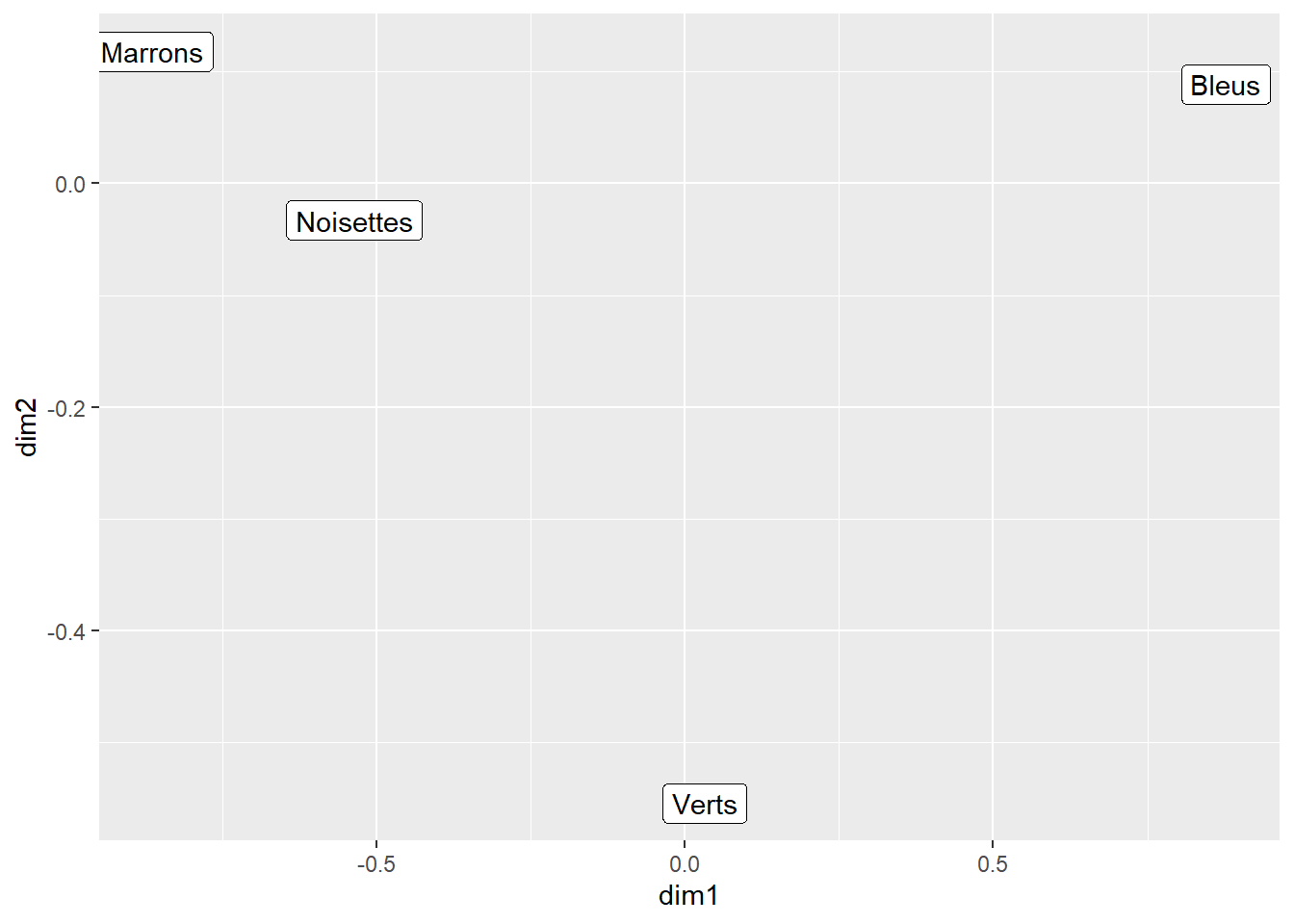
Figure 4.1: Représentation de l’analyse directe
4.2.2 Analyse duale (colonnes)
L’analyse duale est effectuée sur les profils colonnes. Les lignes de \(C = D_p^{-1}F^\top\) sont des éléments de \(\mathbb{R}^n\). On cherche à les représenter dans cet espace muni de la fonction de distance \(x^\top D_n^{-1} x.\)
Dans l’analyse duale, on cherche le vecteur \(v \in \mathbb{R}^n\) tel que \[(v^\top D_n^{-1}F D_p^{-1})D_p(D_p^{-1}F^\top D_n^{-1}v)\] soit maximal, sachant que \(v^\top D_n^{-1}v = 1\).
On trouve la solution en utilisant la proposition A.3 (avec \(A = D_n^{-1}FD_p^{-1} F^\top D_n^{-1}\) et \(M = D_n^{-1}\)). La solution est donnée par le vecteur propre principal de \[D_n (D_n^{-1}FD_p^{-1} F^\top D_n^{-1}) = FD_p^{-1}F^\top D_n^{-1}\equiv T.\]
Calculons \(T\)3
# Matrice dont on cherche les vecteurs propres dans l'analyse directe
TT <- fij_mat %*% solve(Dp) %*% t(fij_mat) %*% solve(Dn)Et calculons ses valeurs propres et vecteurs propres:
| 1 | 0.19 | 0.01 | 0 |
| -0.57 | -0.60 | -0.44 | -0.57 |
| -0.29 | -0.19 | 0.06 | 0.80 |
| -0.22 | 0.01 | 0.79 | -0.18 |
| -0.73 | 0.78 | -0.42 | -0.06 |
Observez les valeurs propres de \(S\) (tableau 4.10) et de \(T\) (tableau 4.12). Vous remarquerez qu’elles sont exactement les mêmes. En fait, si \(p \le n\), les \(p\) premières valeurs propres de \(S\) et de \(T\) coïncident. Cette dernière remarque est assez importante et sa démonstration est présentée dans la section 4.7.2 ]
Le \(j^{\rm e}\) facteur de l’analyse duale est défini par \[\Psi_j = D_n^{-1}v_j, \quad 1 \le j \le p.\]
Les projections des profils des colonnes (c’est-à-dire leurs coordonnées) sur le \(j^{\rm e}\) vecteur propre \(v_j\) sont les composantes du vecteur \[D_p^{-1}F^\top D_n^{-1}v_j = D_p^{-1}F^\top \Psi_j.\]
On peut représenter les profils-colonnes sur les deux dimensions de l’analyse des correspondances.
dat2 <- data.frame(dim1 = coord_col2, dim2 = coord_col3)
ggplot() +
geom_label(aes(dim1,dim2, label = c('Châtains','Roux','Blonds')),dat2)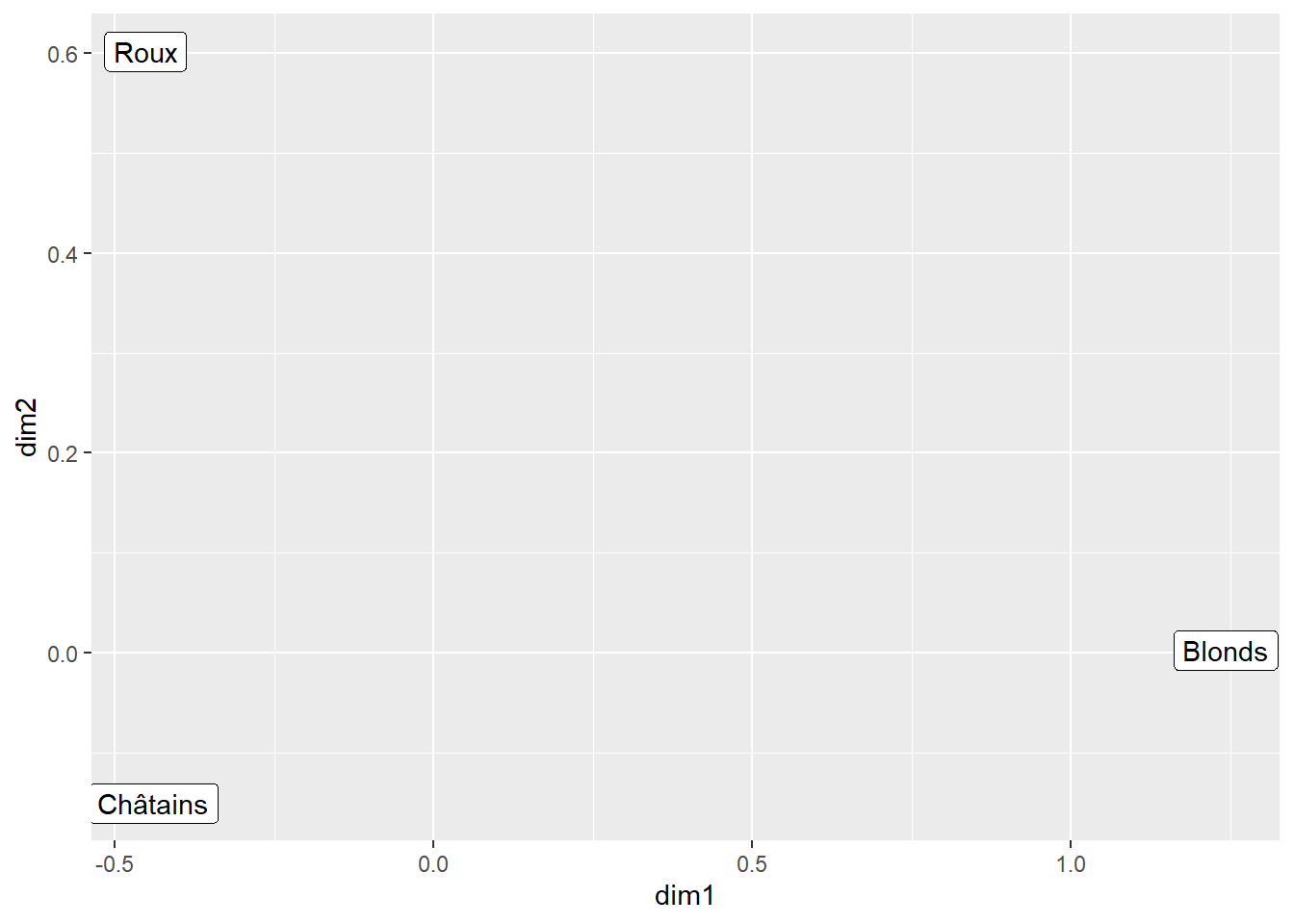
Figure 4.2: Représentation de l’analyse duale
4.2.3 Projection des deux analyses dans le même plan
Le but usuel de l’analyse des correspondances est de produire un graphique en 2 dimensions qui résume l’information contenue dans le tableau de fréquences et qui fait bien ressortir les différentes associations intéressantes. Autrement dit, on veut, en quelque sorte, superposer les figures 4.1 et 4.2.
Pour être en mesure de présenter les deux analyses dans un même plan, il faut s’assurer que les deux ACP projettent les données dans les mêmes dimensions. Les relations de transitions et la notion de centre de gravité présentées dans les deux sections suivantes nous permettent de nous assurer que nous projetons effectivement les «individus» des analyses duales et directes dans les mêmes dimensions.
Relations de transition
Les relations suivantes
\[ \begin{align} D_n^{-1}F \varphi_j &= \sqrt{\lambda_j} \Psi_j \equiv {\hat \Psi}_j \\ D_p^{-1} F^\top \Psi _j &= \sqrt{\lambda}_j \varphi_j \equiv {\hat\varphi}_j \end{align} \]
établissent un lien quasi barycentrique entre les deux types d’analyse, c.-à-d. que les coordonnées des points d’un espace sont proportionnelles aux composantes du facteur de l’autre espace correspondant à la même valeur propre.
Vérification: La première relation se vérifie comme suit. \[ \begin{align*} D_n^{-1}F\varphi_j &= D_n^{-1}(FD_p^{-1}u_j) \\ &= D_n^{-1}(\sqrt{\lambda_j} v_j) = \sqrt{\lambda_j} \Psi_j. \end{align*} \]
La seconde identité se démontre de façon semblable.
Les conséquences des relations de transition précédentes sont que …
- \(1 = \lambda_1 \ge \lambda_2 \ge \cdots \ge \lambda_p \ge 0\).
- \((f_{\bullet 1}, \ldots, f_{\bullet p})^\top\) est un vecteur propre associé à la valeur propre \(\lambda_1 = 1\) de \[S = F^\top D_n^{-1} F D_p^{-1}.\]
Notez que puisque la première valeur propre est toujours égale à un, bien des logiciels ne mentionnent que les \(p-1\) autres valeurs propres.
Centre de gravité
Pour projeter les observations dans un même plan, on doit déterminer l’origine du graphique.
Le centre de gravité des lignes est défini par \(G_L = (g_1, \ldots , g_p)^\top\), où
\[ \begin{equation} g_j = \sum_{i=1}^n f_{i \bullet} \, \frac{f_{ij}}{f_{i \bullet}} = \sum_{i=1}^n f_{ij} = f_{\bullet j} \, , \quad 1 \le j \le p. \end{equation} \]
De même, le centre de gravité des colonnes est défini par
\[ \begin{equation} G_C = (f_{1 \bullet}, \ldots , f_{n \bullet})^\top. \end{equation} \] Le centrage des lignes est obtenu en calculant \[\frac{f_{ij}}{f_{i \bullet}} - g_{j} = \frac{f_{ij}}{f_{i \bullet}} - f_{\bullet j} = \frac{f_{ij} - f_{i \bullet} f_{\bullet j}}{f_{i \bullet}} \, \] de sorte que \[\sum_{j=1}^p \frac{f_{ij} - f_{i \bullet} f_{\bullet j}}{f_{i \bullet}} = 0 \] pour tout \(i \in \{ 1, \ldots , n \}\). La conséquence du centrage des lignes est que l’analyse ne se fait plus sur \[S = F^\top D_n^{-1} F D_p^{-1},\] mais plutôt sur \(S^* = (s^*_{jj^\prime})\), où
\[s_{jj^\prime}^* = \sum_{i=1}^n \frac{(f_{ij} - f_{i \bullet}f_{\bullet j})(f_{ij^\prime} - f_{i \bullet}f_{\bullet j^\prime})}{f_{i \bullet} f_{\bullet j^\prime}} \, .\]
Pour détecter les associations entre lignes et colonnes, il faut faire le lien avec la statistique du test du \(\chi^2\).
Par définition, \[ \begin{equation} \mbox{trace} (S^*) = \sum_{j=1}^p \sum_{i=1}^n \frac{(f_{ij} - f_{i\bullet} f_{\bullet j})^2 }{f_{i \bullet}f_{\bullet j}} \, . \tag{4.1} \end{equation} \]
On retrouve l’expression de la statistique \(Z^2\) (voir section 4.1.5) servant à tester l’indépendance entre deux variables!
Quelques remarques supplémentaires:
- On peut montrer que \(S\) et \(S^*\) les mêmes \(p\) premiers vecteurs propres normalisés.
- \(G_L\) est le vecteur propre de \(S\) associé à sa valeur propre unitaire.
- \(G_L\) est un vecteur propre de \(S^*\) associé à la valeur propre 0.
4.3 En pratique
Plusieurs librairies R permettent de faire l’analyse des correspondances binaires:
| Librairie | Fonction |
|---|---|
| MASS | corresp |
| ca | ca |
| ade4 | dudi.coa |
| FactoMineR | CA |
Nous nous contenterons de montrer l’utilisation de la version proposée par FactoMineR car il s’agit, à ma connaissance et en date de septembre 2018, de la librairie la plus complète pour l’analyse factorielle. La fontcion permettant de faire l’ACB est CA.
Avant de faire l’analyse des correspondances binaires, il peut être pertinent de faire un test du \(\chi^2\) avant de faire l’analyse des correspondances binaires, pour vérifier s’il y a un lien significatif entre les deus variables catégorielles. On obtient le résultat du test avec:
FALSE
FALSE Pearson's Chi-squared test
FALSE
FALSE data: kij
FALSE X-squared = 97.822, df = 6, p-value < 2.2e-16Dans l’exemple 4.1, le test est significatif et le sens du lien est évident. Voici le résultat de l’ACB sur les mêmes données.
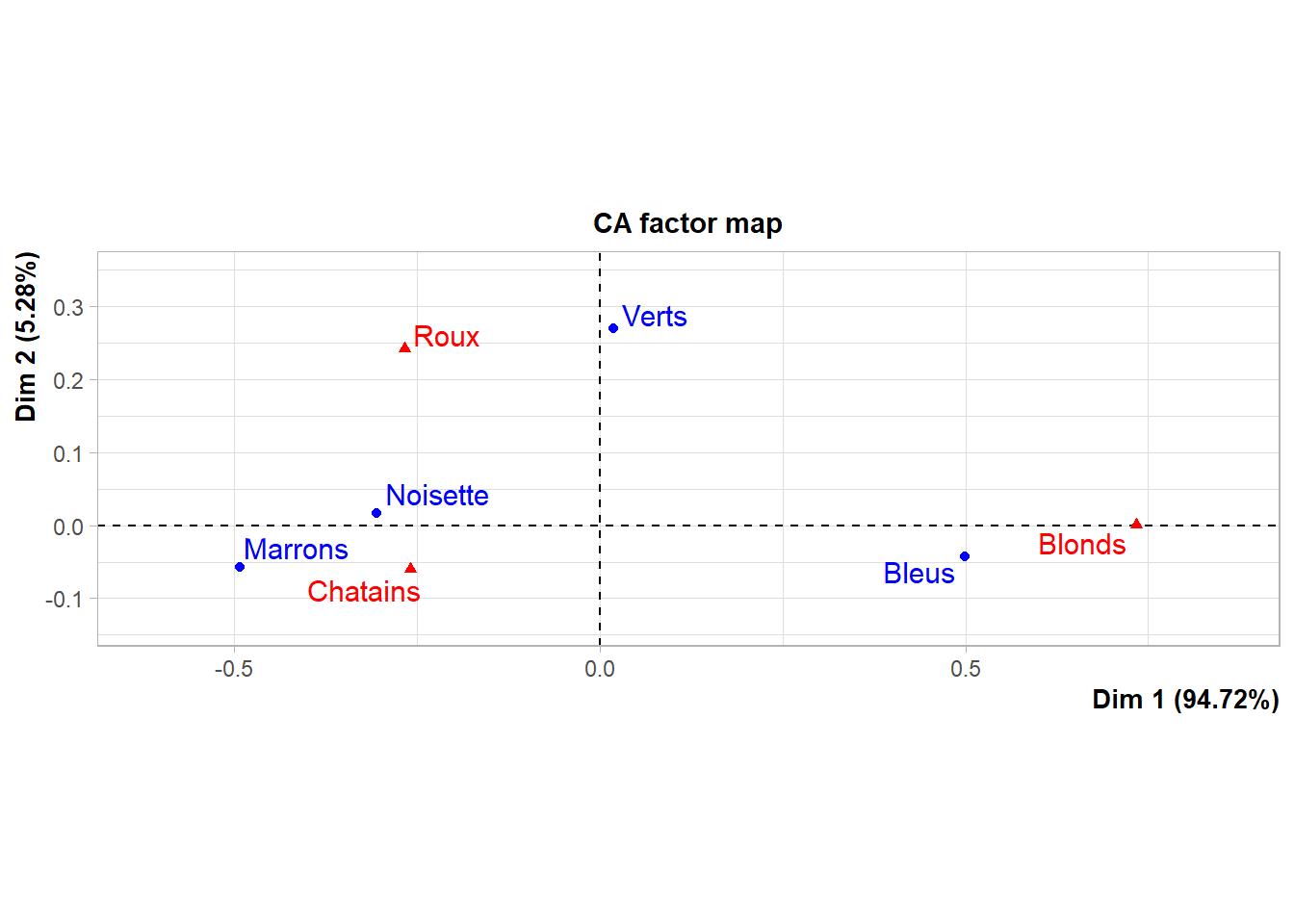
Figure 4.3: Visualisation du lien entre la couleur des cheveux et des yeux avec l’analyse des correspondances binaires
L’interprétation de la figure 4.3 est assez simple: les modalités proches sont des combinaisons de modalités plus fréquentes que ce à quoi on se serait attendu sous l’indépendance. Exprimé autrement, les modalités de deux variables sont proches si elles correspondent à peu près aux mêmes individus. Dans l’exemple, on voit que les modalités «cheveux blonds» et «yeux bleus» sont très près l’une de l’autre. Ceci correspond bien à ce que l’on observe en comparant le tableau des fréquences relatives (4.2) à celui des fréquences relatives attendues sous l’indépendance (4.8): la proportion de personnes aux cheveux blonds et aux yeux bleus est plus grande que ce à quoi on se serait attendu sous l’indépendance.
Dans le plan factoriel, le centre correspond au profil moyen des deux variables. En général, on s’intéresse davantage aux modalités qui s’éloignent du centre de gravité qu’à celles au centre. Il s’agit aussi des modalités qui contribuent le plus aux axes.
L’objet retourné par la fonction CA a une structure similaire à celui retourné par la fonction PCA présentée au chapitre sur l’analyse en composante principale. On peut en extraire les coordonnées des lignes (ici, la couleur des yeux) et des colonnes (ici, la couleur des cheveux) ainsi que la contribution et la qualité de la représentation de chaque modalités sur chacun des axes.
4.3.1 Coordonnées
Les coordonnées des points lignes correspondent au profils lignes projetés sur les axes factoriels (voir la section 4.2.1). La coordonnée de la \(i^e\) ligne sur l’axe \(j\) est donné par la \(i^e\) ligne de:
\[D_n^{-1}F \varphi_j.\] Les coordonnées des points colonnes correspondent au profils colonnes projetés sur les axes factoriels (voir la section 4.2.2). La coordonnée de la \(k^e\) colonne sur l’axe \(j\) est donné par la \(k^e\) ligne de:
\[D_p^{-1}F^\top \psi_j.\]
On retrouve ces valeurs dans le sortie de la fonctionCA:
4.3.2 Contribution et inertie
L’inertie est une moyenne pondérée des carrés des distances des points à leur centre. Elle correspond à la statistique du \(\chi^2\) multipliée par le total des effectifs. Nous avons vu qu’une valeur élevée (plus élevée que ce à quoi on s’attend sous l’indépendance) de la statistique du \(\chi^2\) correspond à un lien significatif entre les deux variables (section 4.1.5). Ainsi, une valeur élevée de l’inertie correspond à un fort lien entre les variables.
Nous avons aussi vu le lien entre la matrice \(S\) et la statistique du \(\chi^2\) (équation (4.1)). Chaque modalité contribue à la statistique du \(\chi^2\) et, conséquemment à l’inertie totale. Cette contribution est proportionnelle à la distance d’un point à l’origine. Plus la coordonnée d’une modalité est élevée (en valeur absolue) sur cet axe, plus sa contribution à l’inertie de cet axe est grande.
Mathématiquement, on définit l’inertie absolue du \(i^e\) point-ligne sur l’axe \(j\) par \[f_{i \bullet} {\hat \Psi}^2_{ji}.\]
Ainsi, la contribution (parfois appelée inertie relative) du \(i^e\) point-ligne sur l’axe \(j\) est \[\frac{f_{i \bullet} {\hat \Psi}^2_{ji}}{\lambda_j} \, .\]
Similairement, l’inertie absolue du \(k^{\rm e}\) point-colonne sur l’axe \(j\) est \[f_{ \bullet k} {\hat \varphi}^2_{jk}.\]
et sa contribution est: \[\frac{f_{ \bullet k} {\hat \varphi}^2_{jk}}{\lambda_j} \, .\]
On obtient ces valeurs dans la sortie de CA:
FALSE Dim 1 Dim 2
FALSE Marrons 39.61802441 9.702975
FALSE Noisette 7.83785136 0.384131
FALSE Verts 0.02142444 82.891349
FALSE Bleus 52.52269979 7.021546FALSE Dim 1 Dim 2
FALSE Chatains 20.772626 20.136464977
FALSE Roux 5.469767 79.860811862
FALSE Blonds 73.757607 0.0027231614.3.3 Qualité de la représentation
La qualité de la représentation d’une modalité est liée à la distance entre les coordonnées de cette modalité et les axes du graphique. On la mesure par le cosinus de l’angle entre le point et l’axe en question.
En fait dans \(\mathbb{R}^n\) muni de la métrique \(D_n^{-1}\), \[d^2(k,G_C) = \sum_{i=1}^n \frac{1}{f_{i \bullet}} \, \left( \frac{f_{ik}}{f_{\bullet j}} - f_{i \bullet} \right)^2 \] est (le carré de) la distance entre \(G_C\) et le \(k^{\rm e}\) point- colonne. Le carré de la projection du \(k^{\rm e}\) point-colonne sur l’axe \(j\) vaut \[d^2_j(k,G_C) = \left( \sqrt{\lambda_j} \varphi_{jk} \right)^2\] et \[\sum_{j=1}^p d^2_j(k,G_C) = \sum_{j=1}^p \left( \sqrt{\lambda_j} \varphi_{jk} \right)^2 = d^2(k,G_C). \] La qualité de la représentation du \(k^{\rm e}\) point-colonne dans l’axe \(j\) est donnée par \[\frac{d^2_j(k,G_C)}{d^2(k,G_C)} = \cos^2 (\theta_{kj}),\] où \[ \begin{align*} \theta_{kj} &= \mbox{angle entre le point } k \mbox{ et}\\ & \,\,\,\,\,\,\,\,\, \mbox{ sa projection sur l'axe } j. \end{align*} \] Plus les \(\cos^2 (\theta_{kj})\) sont élevés, plus l’angle entre les points et l’axe est près de zéro et mieux les points sont représentés sur l’axe \(j\).
Bien sûr une définition analogue existe pour les points-ligne. On peut sommer les qualités d’un même point sur plusieurs axes pour obtenir la qualité total de la représentation de ce point par ces axes. Par exemple on définit \[\mbox{Qualité} = \sum_{i=1}^N \cos^2 (\theta_{ij})\] pour le \(i^{\rm e}\) point-ligne.
On obtient la qualité de la représentation de chaque modalité dans la sortie de la fonction CA:
FALSE Dim 1 Dim 2
FALSE Marrons 0.986520755 0.013479245
FALSE Noisette 0.997273260 0.002726740
FALSE Verts 0.004611535 0.995388465
FALSE Bleus 0.992597032 0.007402968FALSE Dim 1 Dim 2
FALSE Chatains 0.9486943 5.130567e-02
FALSE Roux 0.5511040 4.488960e-01
FALSE Blonds 0.9999979 2.059742e-06En général, s’en tient à interpréter uniquement les modalités les mieux représentées dans le plan (sur les deux axes).
FALSE [1] 39.707544.4 Exemples: exportations vers les États-Unis
L’exemple sur la couleur des yeux et des cheveux est un exemple qui permet de comprendre la méthode, mais qui n’est pas particulièrement réaliste: les liens sont rarement aussi évidents. Voici un exemple plus réaliste qui porte sur les exportations de chaque province canadienne vers les États-Unis. Les données proviennent de Statistique Canada. L’objectif est de visualiser le lien entre les provinces et les catégories d’exportations.
# Téléchargement des données
library(CANSIM2R)
dfraw <- getCANSIM("12-10-0098", lang = 'fra',raw = TRUE)# Manipulation des données
commerceEU <- dfraw %>%
# Renomer les variables
mutate(SCIAN = `Système.de.classification.des.industries.de.l.Amérique.du.Nord..SCIAN.`,
Provinces = `GÉO`) %>%
# Sélectionner 2017 seulement
filter(`X.U.FEFF.PÉRIODE.DE.RÉFÉRENCE` == 2017) %>%
# Sélectionner le nombre d'établissements ou la valeur des exportations selon l'objectif
#filter(Estimations == 'Nombre d\'établissements exportatrices') %>%
filter(Estimations == 'Valeur des exportations') %>%
# Ne conserver que les variables utiles (Province, catégorie SCIAN et valeur des exportations)
select(Provinces, SCIAN, VALEUR) %>%
# Nous supposerons que les valeurs manquantes sont des zéros
replace_na(list(VALEUR = 0)) %>%
# Enlever les lignes correspondant à un total
filter(Provinces != 'Canada') %>%
filter(SCIAN != 'Ensemble des branches d\'activité') %>%
# Mettre le tableau en format large
spread(Provinces, VALEUR, fill = 0) %>%
# Transformer la colonne var en nom de ligne
column_to_rownames(var = 'SCIAN')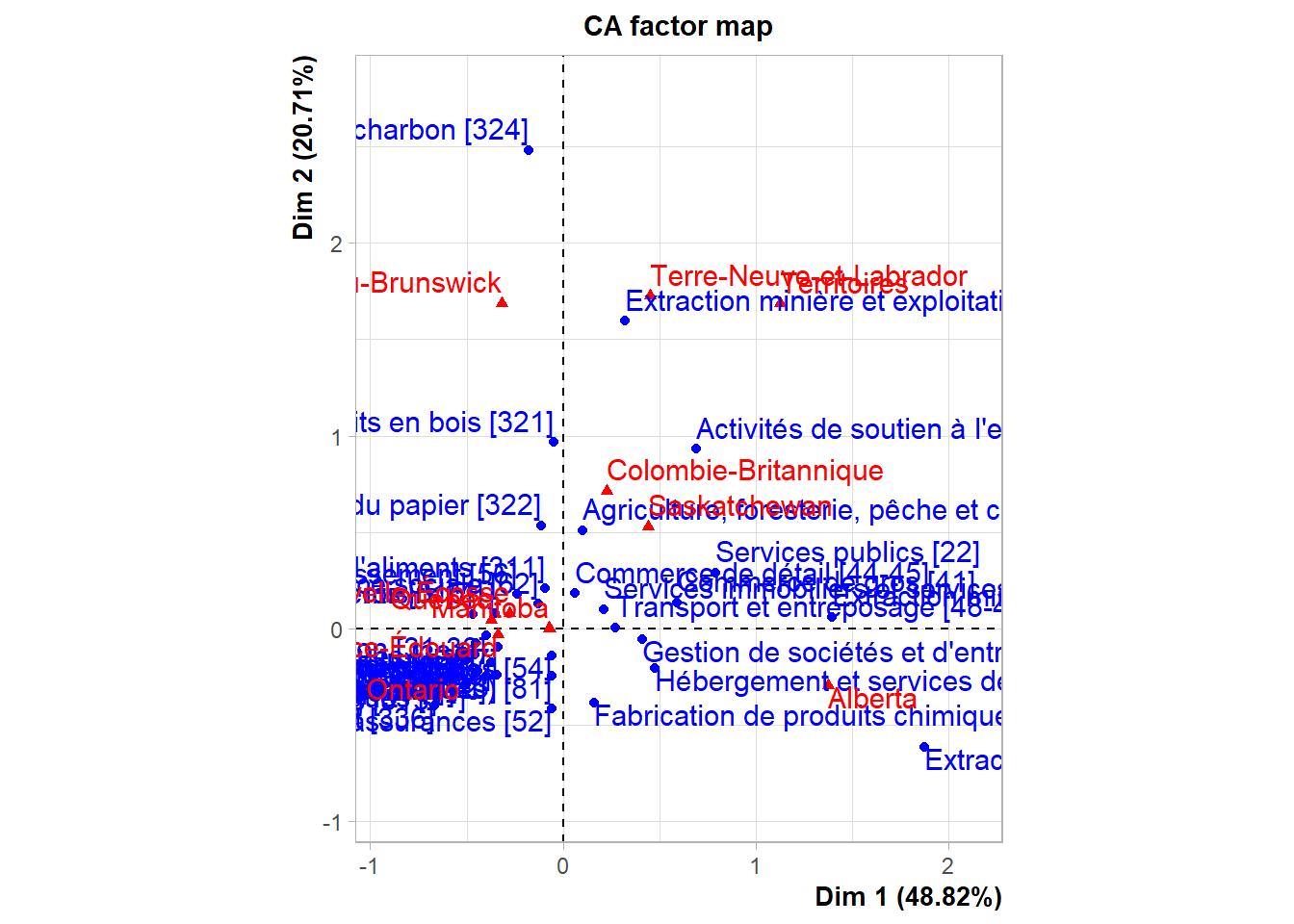
Figure 4.4: Resprésentation des exportations vers les États-Unis par Province
La figure 4.4 est illisible et n’est, conséquemment, d’aucune utilité. Il faut nécessairement la retravailler un peu et la présenter en format interactif. Un autre élément qui aide à l’interprétation est la qualité. La fonction graphCA (voir C.1) permet de visualiser le résultat de l’analyse des correspondances de façon interactive en plus de voir la qualité de la représentation de chaque modalité dans ce plan (cette valeur est simplement la somme des qualités sur les deux axes représentés).
La figure est encore un peu trop lourde pour être interprétée facilement. Dans un premier temps, nous allons faire le ménage des modalités. Certaines modalités sont redondantes. Par exemple, la modalité Extraction de pétrole et de gaz est incluse dans la modalité Extraction minière et exploitation en carrière. Ensuite, nous allons retirer les branches d’activités qui représentent moins d’un milliard d’exportations annuellement, regrouper les provinces maritimes et retirer les territoires.
commerceEU2 <- commerceEU %>%
rownames_to_column('SCIAN') %>%
filter(rowSums(commerceEU) > 1000000) %>%
# filter(SCIAN != 'Ensemble des branches d\'activité')%>%
filter(SCIAN != 'Extraction de pétrole et de gaz') %>%
filter(SCIAN != 'Extraction minière et exploitation en carrière (sauf l\'extraction de pétrole et de gaz)') %>%
mutate(Maritimes = `Île-du-Prince-Édouard` + `Nouveau-Brunswick` + `Nouvelle-Écosse` + `Terre-Neuve-et-Labrador`) %>%
select(-`Île-du-Prince-Édouard`, -`Nouveau-Brunswick`, -`Nouvelle-Écosse`, -`Terre-Neuve-et-Labrador`, -Territoires) %>%
column_to_rownames(var = 'SCIAN')
# Renommer les lignes
rownames(commerceEU2)[c(1,7)] <- c( 'Soutien extraction (mine, petrole et gaz)', 'Extraction petrole, gaz, mines')On voit clairement le lien entre les l’Alberta et l’exploitation du pétrole ainsi que celui entre les provinces maritimes et la fabrication de produits du pétrole et du charbon.
Ici, on voit que le deuxième axe est fortement lié à deux modalités en particulier (Maritimes et Fabrication de produits du pétrole et du charbon). Observons la contribution de chaque colonne aux différents axes:
kable(commerceEU2_CA$col$contrib,
Caption = "Contribution de chaque colonne aux axes factoriels",
digit = 2)| Dim 1 | Dim 2 | Dim 3 | Dim 4 | Dim 5 | |
|---|---|---|---|---|---|
| Alberta | 71.10 | 7.17 | 1.79 | 0.35 | 0.01 |
| Colombie-Britannique | 0.58 | 30.88 | 29.49 | 18.83 | 5.70 |
| Manitoba | 0.02 | 0.31 | 2.93 | 33.10 | 13.20 |
| Ontario | 22.77 | 16.50 | 0.40 | 0.09 | 16.60 |
| Québec | 4.42 | 0.26 | 0.60 | 4.49 | 60.09 |
| Saskatchewan | 0.94 | 7.52 | 8.70 | 42.77 | 4.08 |
| Maritimes | 0.17 | 37.35 | 56.09 | 0.37 | 0.32 |
On voit que les maritimes contribuent très fortement au deuxième axe. On peut voir le même phénomène sur les lignes avec la fabrication de produits du pétrole et du charbon.
En général en ACB, on n’étudie que les deux premiers axes. Dans l’exemple, puisque le deuxième axe est trop lié à la fabrication de produits du pétrole, nous allons nous intéresser au troisième axe.
4.5 Analyse des correspondances multiples
L’analyse des correspondances multiple sert à résumer, dans un graphique en 2 dimensions, les associations présentent dans des tableaux de fréquences croisant plus de deux variables. Cette analyse est particulièrement populaire pour faire une première analyse exploratoire d’enquêtes ou d’études faites à partir de questionnaires formés de plusieurs questions à choix multiples.
4.5.1 Notation et codification des données
4.5.1.1 Tableau disjonctif complet
Nous nous concentrerons dans ce cours sur l’analyse de questionnaires à choix multiples. Il faut coder les données d’une façon similaire à celle qui suit:
| Individu | AS | AJ | ES | EJ | SE | NON | MOY | GRO | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | |
| 2 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | |
| 3 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | |
| 4 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) | |
| 193 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
Dans l’exemple précédent, le nombre de questions \(Q\) est égal à deux. On a ainsi un tableau de la forme suivante. \[Z = [ Z_1 ~|~ Z_2 ].\]
En général, pour un questionnaire contenant \(Q\) questions, on a un tableau de la forme \[Z = [Z_1 ~|~ \cdots ~|~ Z_Q ].\]
Un peu de notation additionnelle: \[\begin{align*} Q &= \mbox{nombre de questions}\\ n &= \mbox{nombre d'individus répondant au questionnaire}\\ p_q &= \mbox{nombre de modalités de la question } q\\ p &= p_1 + \cdots + p_Q \end{align*}\]
Il est à noter que plus \(Q\) est grand, plus il y aura de cellules vides; en fait, la proportion de cellules non vides est \[\frac{nQ}{np} = \frac{Q}{p} \, .\]
Dans le cas particulier où toutes les questions ont le même nombre de choix de réponses, on a \[p_1 = \cdots = p_Q = \frac{p}{Q} \, ,\] de sorte que \[\frac{Q}{p} = \frac{1}{p_1} \to 0 \mbox{ quand } p_1 \to \infty.\]
4.5.1.2 Tableau de Burt
C’est une autre faon de présenter un tableau de fréquences contenant plus de deux variables. Étant donné un tableau logique \[Z = [ Z_1 ~|~ \cdots ~|~Z_Q],\]
le tableau de Burt associé à ce tableau logique est la matrice carrée \(p \times p\) définie comme étant
\[B = Z Z^\top \]
\[B = \left[ \begin{array}{cccc} Z_1^\top Z_1 & Z_1^\top Z_2 & \cdots & Z_1^\top Z_Q \\ Z_2^\top Z_1 & Z_2^\top Z_2 & \cdots & Z_2^\top Z_Q \\ \vdots & \vdots & \cdots & \vdots \\ Z_Q^\top Z_1 & Z_Q^\top Z_2 & \cdots & Z_Q^\top Z_Q \\ \end{array} \right]. \]
Quelques remarques sur la forme de \(Z_q^\top Z_{q^\prime}\) …
- \(Z_q^\top Z_q\) est une matrice diagonale \(p_q \times p_q\) présentant les réponses à la \(q^{\rm e}\) question.
- L’élément \((j,j)\) de la matrice \(Z_q^\top Z_q\) est égal au nombre d’individus \(d_{jj}\) qui appartiennent à la \(j^{\rm e}\) catégorie de la \(q^{\rm e}\) question.
- \(Z_q^\top Z_{q^\prime}\) est le tableau de fréquences présentant les réponses aux \(q^{\rm e}\) et \(q^{\prime \rm e}\) questions. L’élément \((j,j^{\prime})\) de la matrice \(Z_q^\top Z_{q^\prime}\) est égal au nombre d’individus \(d_{jj^{\prime}}\) qui appartiennent à la \(j^{\rm e}\) catégorie de la \(q^{\rm e}\) question et à la \(j^{\prime \rm e}\) catégorie de la \(q^{\prime \rm e}\) question.
Si on retourne à l’exemple précédent, on obtient le tableau du Burt qui suit.
| AS | AJ | ES | EJ | SE | NON | MOY | GRO | ||
|---|---|---|---|---|---|---|---|---|---|
| AS | 11 | 0 | 0 | 0 | 0 | 4 | 5 | 2 | |
| AJ | 0 | 18 | 0 | 0 | 0 | 4 | 10 | 4 | |
| ES | 0 | 0 | 51 | 0 | 0 | 25 | 22 | 4 | |
| EJ | 0 | 0 | 0 | 88 | 0 | 18 | 57 | 13 | |
| SE | 0 | 0 | 0 | 0 | 25 | 10 | 13 | 2 | |
| NON | 4 | 4 | 25 | 18 | 10 | 61 | 0 | 0 | |
| MOY | 5 | 10 | 22 | 57 | 13 | 0 | 107 | 0 | |
| GRO | 2 | 4 | 4 | 13 | 2 | 0 | 0 | 25 |
On pose \(D_i = Z_i^\top Z_i\) et \[D = \left[ \begin{array}{ccccc} Z_1^\top Z_1 & 0 & 0 & \cdots & 0\\ 0 & Z_2^\top Z_2 & 0 & \cdots & 0 \\ 0 & 0 & Z_3^\top Z_3 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & Z_Q^\top Z_Q \\ \end{array} \right] \]
4.5.2 Mathématique de l’ACM
D’un point de vue mathématique, l’analyse des correspondances multiples est une analyse des correspondances binaires effectuée sur la matrice logique \(Z\) ou sur le tableau de Burt \(B\). Nous allons montrer que l’on obtient les mêmes facteurs, et ce, peu importe la matrice utilisée pour l’analyse.
Pour l’analyse des correspondances binaires, on avait \[F = \left( F_{ij} \right).\] Pour l’analyse des correspondances multiples avec la matrice \(Z\), on a \[F = \frac{Z}{nQ}\] avec
\[\sum_{i=1}^n \sum_{j=1}^p f_{ij} = \sum_{i=1}^n \sum_{j=1}^p \frac{Z_{ij}}{nQ} = 1. \]
Pour l’analyse des correspondances multiples avec le tableau de Burt, on a \[F = \frac{B}{nQ^2},\] puisque chacun des \(Q\) blocs de \(B\) est composé d’entiers dont la somme est égale à \(n\). De plus, \(B\) est une matrice symétrique. L’analyse des correspondances multiples avec le tableau de Burt est effectuée avec \(n=p\).
Dans ce cas particulier, on a
\[ D_n = D_p = \displaystyle \frac{D}{nQ}. \]
Les facteurs de l’analyse des correspondances multiples avec le tableau de Burt sont donnés par l’équation \[\varphi_j^* = D_n^{-1}v_j = nQ D^{-1}v_j,\] où \[FD_p^{-1}F^\top D_n^{-1} v_j = \lambda^*_j v_j.\] De façon équivalente, on a \[\frac{1}{Q^2} \, BD^{-1}B^\top D^{-1} v_j = \lambda^*_j v_j.\] Le facteur \(\varphi^*_j\) est la solution de l’égalité \[\frac{1}{Q^2} \, BD^{-1} B^\top \varphi_j^* = \lambda^*_j D \varphi_j^*, \] ou encore, en multipliant les deux côtés de l’équation par \(D^{-1}\), le facteur \(\varphi^*_j\) est la solution de l’égalité
\[\frac{1}{Q^2} \, D^{-1}BD^{-1}B^\top \varphi_j^* = \lambda_j^* \varphi^*_j. \]
En ce qui concerne l’analyse basée sur la matrice \(Z\), on sait que \[\frac{1}{Q} \, D^{-1} B^\top \varphi_j = \lambda_j \varphi_j,\]
de sorte qu’en multipliant les deux c^otés de l’égalité par \(D^{-1}B/Q\), on obtient que
\[\frac{1}{Q^2} \, D^{-1}BD^{-1}B^\top \varphi_j = \lambda_j \frac{D^{-1}B\varphi_j}{Q} = \lambda_j^2 \varphi_j. \]
On en conclut donc que \[ {\lambda^*_j = \lambda_j^2}, \quad 1 \le j \le p \quad \mbox{et que} \quad {\varphi^*_j = \varphi_j}, \quad 1 \le j \le p.\]
Dans le cas où \(Q=2\), l’analyse des correspondances multiples avec la matrice \(Z\) est équivalente à l’analyse des correspondances binaires avec la matrice \(Z_2^\top Z_1\). En fait, le \(j^{\rm e}\) vecteur \(\Phi_j\) de l’analyse des correspondances multiples avec la matrice \(Z=[Z_1~|~Z_2]\) est de la forme \[\Phi_j = \left( \varphi_j , \psi_j \right)^\top,\]
où \(\varphi_j\) et \(\psi_j\) sont respectivement les \(j^{\rm e}\) facteurs direct et dual de l’analyse de \(Z_2^\top Z_1\).
Si \[\lambda_j^* = j^{\rm e} \mbox{ valeur propre issue de } Z_2^\top Z_1,\] alors \[\lambda_j = \frac{1+ \sqrt{\lambda_j^*}}{2} \, , \quad 1 \le j \le p.\]
4.5.3 Interprétation
On crée un graphique comme pour l’analyse des correspondances binaires. L’interprétation du graphique est similaire, mais pas tout à fait exactement la même. En fait,
- on s’intéresse aux points qui sont dans une même région ou dans un même quadrant du graphique;
- on s’intéresse aux points qui sont dans une même direction par rapport à l’origine.
4.5.4 En pratique
L’analyse des correspondances multiples se fait avec la fonction MCA de la librairie FactoMineR. La syntaxe et la sortie sont similaires à celles de l’ACP et de l’ACB.
L’exemple qui nous permettra d’illustrer l’ACP provient d’un sondage web volontaire effectué par Kaggle auprès de ses utilisateurs. Les données sont disponibles ici. Nous nous en tiendrons à trois variables:
- le langage de programmation recommandé (lang)
- le principal domaine d’étude (discipline)
- le niveau de scolarité (scolarite)
# Contient les réponses au sondage
kaggle <- read_csv(file = "don/multipleChoiceResponses.csv")
# Sélectionner les variables et les modalitées et retirer les NA
kaggle2 <- kaggle %>%
select( lang = LanguageRecommendationSelect, discipline = MajorSelect, scolarite = FormalEducation) %>%
filter(lang %in% c('SAS', 'Python', 'R', 'Matlab'),
discipline %in% c("Mathematics or statistics", "Computer Science"),
scolarite != 'I prefer not to answer') %>%
na.omit
# Faire l'ACM
kaggle_MCA <- MCA(kaggle2, graph = FALSE)
# Extraire les coordonnées
coord_col <- as.data.frame(kaggle_MCA$var$coord) %>%
rownames_to_column(var = 'modalite')
# Ajouter le nom des variables
coord_col$variable <- NA
coord_col$variable[1:4] <- 'lang'
coord_col$variable[5:6] <- 'discipline'
coord_col$variable[7:10] <- 'scolarite'
# Extraire la qualité
qualite <- kaggle_MCA$var$cos2[,1] +kaggle_MCA$var$cos2[,2]
# Faire le graphique
g_var <- ggplot() +
geom_point(data = coord_col,
aes(`Dim 1`, `Dim 2`, label = modalite, color = variable, alpha = qualite)) +
theme_minimal()
# Rendre le graphique interactif.
ggplotly(g_var, tooltip = c('modalite', 'qualite'))Figure 4.5: Visualisation des résultats du sondage Kaggle avec l’analyse des correspondances multiples
La figure 4.5 permet de constater que la formation en informatique est liée à la recommandation du langage Python et à un niveau de scolarité correspondant au baccalauréat. La formation en mathématiques ou en statistique est liée à recommandation du langage R. Une autre façon d’exprimer l’interprétation du graphique est de dire que les gens qui ont recommandé le langage R sont, en général, aussi ceux qui ont une formation en mathématiques ou en statistique.
4.6 Extensions de l’analyse des correspondances
L’analyse en composantes principales nous permet d’analyser des variables quantitatives et l’analyse des correspondances (binaires et multiples) nous permet d’analyser des données catégorielles. En pratique, il est assez fréquent de devoir travailler à la fois avec des variables quantitatives et des variables catégorielles. Dans un tel cas, l’une des façons de s’en sortir est de découper les variables continues en intervalles. On obtient ainsi des variables ordinales qu’on peut inclure dans une analyse des correspondances binaires ou multiples.
Voici un exemple pour découper le salaire des répondants au sondage de Kaggle en une variable catégorielle avec R:
# Il faut d'abord ramener le tout dans la même devise.
# Le taux de conversion des devises
conversionRates <- read_csv(file = "don/conversionRates.csv")
# Conversion des devises en $US
compensation <- data.frame(montant = as.numeric(kaggle$CompensationAmount),
devise = kaggle$CompensationCurrency)%>%
left_join(conversionRates, by=c('devise'='originCountry')) %>%
mutate(montantUS = montant*exchangeRate) %>%
select(montantUS)
# Ajout des montants corrigée au jeu complet
kaggle <- kaggle %>%
mutate(CompensationUS = compensation$montantUS) %>%
select(-CompensationAmount, -CompensationCurrency)
# Découper les salaires en trois catégories
kaggle$salaire_cut <- cut(kaggle$CompensationUS, breaks = c(0, 50000, 100000 , Inf), labels = c( "Bas", "Élevé", "Très élevé"))Malheureusement, la transformation des variables continues en variables ordinales peut entraîner une perte d’information. La méthode pour traiter simultanément des données continues et catégorielles a été développée par une Française dans les années 1970 (1979) mais son incorporation dans les librairies est plus récente. On peut maintenant faire ce type d’analyse avec la fonction FAMD de la librairie FactoMineR.
D’autres extensions permettent, par exemple, de grouper des variables ou des individus. Le site web de la librairie FactoMineR contient beaucoup d’information sur les extensions possibles de l’analyse factorielle.
4.7 Compléments
4.7.1 Illustration de la préservation des distances au carré
Voici un petit exemple numérique pour illustrer les remarques précédentes. Considérons un tableau fictif \(2 \times 3\)
| Colonne 1 | Colonne 2 | Colonne 3 | Total | |
|---|---|---|---|---|
| obs1 | 11 | 22 | 16 | 49 |
| obs2 | 16 | 32 | 3 | 51 |
| Total | 27 | 54 | 19 | 100 |
dont les deux premières colonnes ont le même profil. La distance entre les deux premières lignes est
\[\begin{eqnarray*} d^2(1,2) &= & \frac{100}{27} \, \left( \frac{11}{49} - \frac{16}{51} \right)^2 + \frac{100}{54} \, \left( \frac{22}{49} - \frac{32}{51} \right)^2 + \\ & & \frac{100}{19} \, \left( \frac{16}{49} - \frac{3}{51} \right)^2 \\ & = & 0.088~477~88. \end{eqnarray*}\]
Maintenant, additionnons les deux premières colonnes:
| Colonne 1 +Colonne 2 | Colonne 3 | Total | ||
|---|---|---|---|---|
| obs1 | 33 | 16 | 49 | |
| obs2 | 48 | 3 | 51 | |
| Total | 81 | 19 | 100 |
La distance entre les deux premières lignes devient \[\begin{align*} D^2(1,2) &= \frac{100}{81} \, \left( \frac{33}{49} - \frac{48}{51} \right)^2 + \frac{100}{19} \, \left( \frac{16}{49} - \frac{3}{51} \right)^2 \\ \\ &= 0.088~477~88. \end{align*}\]
La démonstration du phénomène illustré dans cet exemple est assez simple. On suppose que \[\frac{f_{ij_1}}{f_{\bullet j_1}} = \frac{f_{ij_2}}{f_{\bullet j_2}} = F_i, \quad 1 \le i \le n. \] Si \(f_{\bullet j_0} = f_{\bullet j_1} + f_{\bullet j_2}\), alors on a, pour tout \(i\), \[\frac{f_{ij_0}}{f_{\bullet j_0}} = \frac{f_{ij_1}+f_{ij_2}}{f_{\bullet j_0}} = \frac{F_i (f_{\bullet j_1} + f_{\bullet j_2} )}{f_{\bullet j_0}} = F_i. \]
On trouve que
\[ d^2(i,i^\prime) - D^2 (i, i^\prime) \equiv \Delta = \] \[\frac{1}{f_{\bullet j_1}} \left( \frac{f_{ij_1}}{f_{i \bullet}} - \frac{f_{i^\prime j_1}}{f_{i^\prime \bullet}} \right)^2 + \frac{1}{f_{\bullet j_2}} \left( \frac{f_{ij_2}}{f_{i \bullet}} - \frac{f_{i^\prime j_2}}{f_{i^\prime \bullet}} \right)^2 - \frac{1}{f_{\bullet j_0}} \left( \frac{f_{ij_0}}{f_{i \bullet}} - \frac{f_{i^\prime j_0}}{f_{i^\prime \bullet}} \right)^2. \] Par conséquent, \[\begin{align*} \Delta &= f_{\bullet j_1} \left( \frac{F_i}{f_{i \bullet}} - \frac{F_{i^\prime}}{f_{i^\prime \bullet}} \right)^2 + f_{\bullet j_2} \left( \frac{F_i}{f_{i \bullet}} - \frac{F_{i^\prime}}{f_{i^\prime \bullet}} \right)^2 -\\ & \quad f_{\bullet j_0} \left( \frac{F_i}{f_{i \bullet}} - \frac{F_{i^\prime}}{f_{i^\prime \bullet}} \right)^2 \\ &= 0. \end{align*}\]
4.7.2 Démonstration de la coïncidence des valeurs propre de \(S\) et \(T\)
Nous allons démonter la dernière affirmation de cette remarque. Si \(Su = F^\top D_n^{-1} F D_p^{-1} u = \lambda u\), alors \[\begin{align*} FD_p^{-1} Su &= FD_p^{-1} F^\top D_n^{-1} (F D_p^{-1} u) \\ &= \lambda (F D_p^{-1} u), \end{align*}\] de sorte que \(v = F D_p^{-1} u\) est un vecteur propre de \(T = FD_p^{-1} F^\top D_n^{-1}\). De plus si \(u\) est associé à \(\lambda\) et si \[u^\top D_p^{-1}u = 1,\] alors \(v = F D_p^{-1} u\) est un vecteur propre de \(T\) et \[\begin{align*} v^\top D_n^{-1} v &= u^\top D_p^{-1}F^\top D_n^{-1}F D_p^{-1}u \\ &= u^\top D_p^{-1} (F^\top D_n^{-1}F D_p^{-1}u) \\ &= \lambda u^\top D_p^{-1}u \\ &= \lambda . \end{align*}\] Il faut donc prendre \[v_j = \frac{1}{\sqrt{\lambda_j}} \, FD_p^{-1}u_j , \quad j \in \{ 1, \ldots , p \}\] pour avoir un vecteur de norme unitaire.
Réciproquement, on a \[u_j = \frac{1}{\sqrt{\lambda_j}} \, F^\top D_n^{-1} v_j, \quad j \in \{ 1, \ldots , p \}. \]
Références
Snee, Ronald D. 1974. “Graphical Display of Two-Way Contingency Tables.” The American Statistician 28 (1): 9–12.