Chapitre 6 Introduction à l’apprentissage supervisé
Les méthodes supervisées consistent à prédire une variable \(Y\) en fonction de variables explicatives \(X\). Évidemment, les exemples d’applications des modèles prédictifs sont nombreux:
- Estimer la valeur d’une maison selon certaines caractéristiques
- Déterminer la probabilité qu’un client achète ou non, qu’un client quitte
- Évaluer le risque (d’accident, de non-conformité…)
- Prédire un volume de précipitation
- Prédire la demande en électricité
- …
Le vocabulaire utilisé pour parler des méthodes supervisées varie selon les disciplines.
En statistique, on utilise souvent le terme régression pour parler de l’ensemble des méthodes associées aux modèles linéaires généralisés. Ainsi, la régression inclut la régression linéaire (\(Y\) continu), la régression logistique (\(Y\) binaire), la régression multinomiale (\(Y\) catégoriel), la régression de Poisson… Les autres méthodes prédictives auront leur propre nom, comme l’analyse discriminante.
Dans le domaine de l’informatique, on sépare l’ensemble des modèles possibles en deux grandes catégories: la régression et la classification. Le sens du mot régression n’est pas le même qu’en statistique. Il réfère à l’ensemble des méthodes permettant de prédire une variable quantitative. La classification réfère quant à elle à l’ensemble des méthodes permettant de prédire une variable catégorielle. Ainsi, dans le domaine de l’informatique, on parlera d’arbre de classification pour les variables binaires et d’arbres de régression pour les variables continues. Le modèle dont il est question dans les arbres de régression n’a rien à voir avec la régression au sens statistique du terme. Dans cet univers parallèle, la régression logistique n’est pas une méthode de régression, mais une méthode de classification. De plus, la classification n’est pas considérée comme une prédiction. Le terme prédiction est réservé à la prédiction d’une variable continue.
À cette confusion viennent s’ajouter les subtilités de la langue française. Notre charmante langue n’attribue pas exactement la même signification au terme classification que la langue anglaise. Le terme anglais classification, devrait être traduit par le terme classement en français. Ainsi, les ouvrages français parlent de méthodes de régression et de classement, le terme classification étant réservé aux méthodes non supervisées.
Heureusement, le langage mathématique étant plus universel, nous pouvons nous en tenir à la formulation suivante: on s’intéresse à \(E(Y|X)\), peu importe la nature de \(Y\) et de \(X\).
6.1 Prédire ou comprendre
Un modèle qui permet de comprendre un phénomène permet généralement de faire une prévision. C’est le cas de la régression linéaire simple. Si l’on a deux variables et qu’on ajuste un modèle de régression par maximum de vraisemblance et on pourra obtenir une prévision pour une nouvelle observation avec \(\hat{y}=\hat{\beta}_0 + \hat{\beta}_1 x_1 + \hat{\beta}_2 x_2\). Si le modèle est bien spécifié et que les postulats sont respectés, nous serons aussi en mesure d’expliquer l’effet de \(X_1\) et de \(X_2\) sur \(Y\) grâce aux coefficients \(\hat{\beta}_1\) et \(\hat{\beta}_2\). Ce pouvoir explicatif de la régression en fait l’un des modèles les plus utilisés.
Dans certaines situations, toutefois, nous ne sommes pas intéressés à comprendre le phénomène. Nous voulons seulement obtenir une bonne prédiction. Ce genre de situation permet d’utiliser toute une autre gamme de modèles qui sont difficiles à interpréter, mais qui permettent de prédire très efficacement la valeur d’une nouvelle observation. Les forêts aléatoires, les réseaux de neurones et les machines à vecteur de support en font partie. On dit parfois que ces modèles sont des «boîtes noires».
La plupart du temps, dans les applications dans le monde de la recherche et du marketing, on cherche à comprendre un phénomène plus qu’à le prédire. Même si un collaborateur affirme avec certitude que son objectif est de prédire si un client va acheter ou pas, deux ou trois questions supplémentaires permettront de découvrir qu’il veut en réalité savoir quel type de personne est plus susceptible d’acheter. Ce genre de situation surviendra dans d’autres domaines. On pourrait par exemple vous dire qu’on a pour objectif de prédire si un patient est susceptible ou non de répondre positivement à un traitement. En creusant un peu vous risquez de découvrir qu’on veut aussi savoir quel type de personne réagit mieux et si cet écart est significatif.
Dans certaines situations, c’est la loi, la réglementation ou les politiques internes d’une entreprise en matière d’éthique qui vous forceront à créer un modèle qui s’interprète. En assurances, par exemple, les actuaires doivent fournir une liste des variables considérées dans le modèle ainsi que leur effet sur la prime. L’Union européenne a récemment instauré une loi sur la protection des renseignements personnels7 qui restreint grandement l’utilisation des données et dont certains articles laissent croire que les modèles purement prédictifs devraient être évités dans certaines situations.
Enfin, il y a des cas où la nature de la décision à prendre est si importante que l’on préfère avoir une bonne compréhension du modèle pour pouvoir s’y fier.
Ainsi, il est très important de se poser sérieusement cette question dès le début d’un projet: est-ce qu’on veut seulement prédire \(Y\) ou est-ce qu’on veut aussi comprendre ce qui unit \(Y\) à \(X\)? Si l’objectif est seulement de prédire, la section suivante offre un excellent outil pour choisir vos modèles.
6.2 Construction du modèle prédictif.
La construction d’un modèle prédictif se fait généralement en trois phases8:
- une phase d’entraînement: On utilise l’échantillon d’entraînement pour créer le modèle. Dans le cas d’un modèle paramétrique, par exemple, c’est dans cette phase que nous estimons les paramètres. En général, on entraîne plusieurs modèles ou plusieurs variantes d’un même modèle.
- une phase de validation: On utilise l’échantillon de validation pour évaluer la performance du modèle sur des données qui n’ont pas servi à l’entraînement, de façon à éviter le surapprentissage. La performance du modèle peut se baser sur différents indicateurs. On choisit le modèle qui obtient la meilleure performance (l’EQM la plus basse) sur l’échantillon de validation.
- une phase de test: On utilise l’échantillon de test pour évaluer la performance finale du modèle. Elle est utile lorsque l’on souhaite une évaluation rigoureuse de la performance finale du modèle.
Cette approche requiert que l’on sépare aléatoirement l’échantillon en trois (un échantillon pour chaque phase). L’échantillon d’entraînement comprend généralement entre 50% et 80% des données. L’échantillon de validation comprend entre 20% et 40% des données et l’échantillon de test utilise entre 5% et 10% des données (il est fréquent, en pratique, que cette étape soit omise).
6.2.1 La validation croisée
La validation croisée est une extension de la validation présentée précédemment. Plutôt que de séparer l’échantillon en un échantillon d’entraînement et un échantillon de validation, on procède de la façon suivante:
Pour tous les modèles:
- On sépare l’échantillon en K groupes de façon aléatoire
- On entraîne un modèle en excluant le premier groupe
- On calcule la performance du modèle sur le premier groupe
On répète les étapes 2 et 3 avec les K groupes.
On fait la moyenne des performances, on choisit le modèle le plus performant.
6.3 Surapprentissage
L’utilisation de données de validation et de test pour choisir un modèle sert à éviter le surapprentissage (ou surentraînement, ou surajustement) d’un modèle. Pour illustrer le concept, deux jeux de données ont été simulés à partir du même modèle (l’un pour l’entraînement et l’autre pour la validation). Nous considérerons que ce modèle est inconnu et nous essaireons de l’approximer par un polynôme. Les figures suivantes présentent les données d’entraînement (rose), les données de validation (vert) et le polynôme ajusté (ligne noire).
La figure 6.1 illustre le modèle qu’on obtient avec un polynôme de degré 1 ajusté sur les données d’entraînement. On voit que ce modèle n’est pas suffisamment complexe pour bien modéliser les données. La figure 6.3 donne quant à elle un exemple de surajustement. Le polynôme d’ordre 5 se montre très bon pour modéliser les données d’entraînement. Il s’ajuste toutefois très mal aux données de validation. Le polynôme d’ordre 2 (figure 6.2) montre un bon compromis. Il s’ajuste à peu près aussi bien aux données d’entraînement qu’aux données de validation.
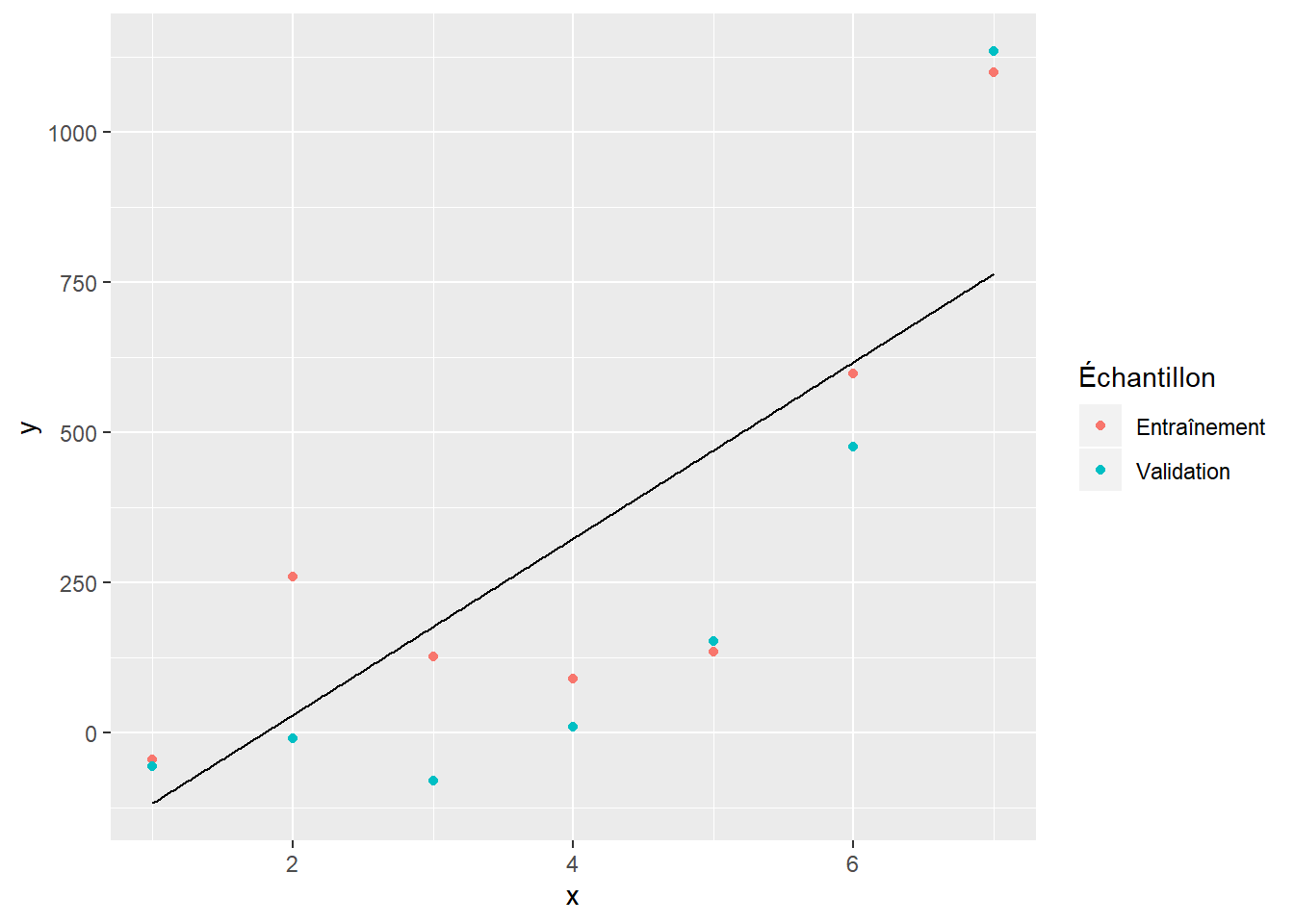
Figure 6.1: Polynôme d’ordre 1
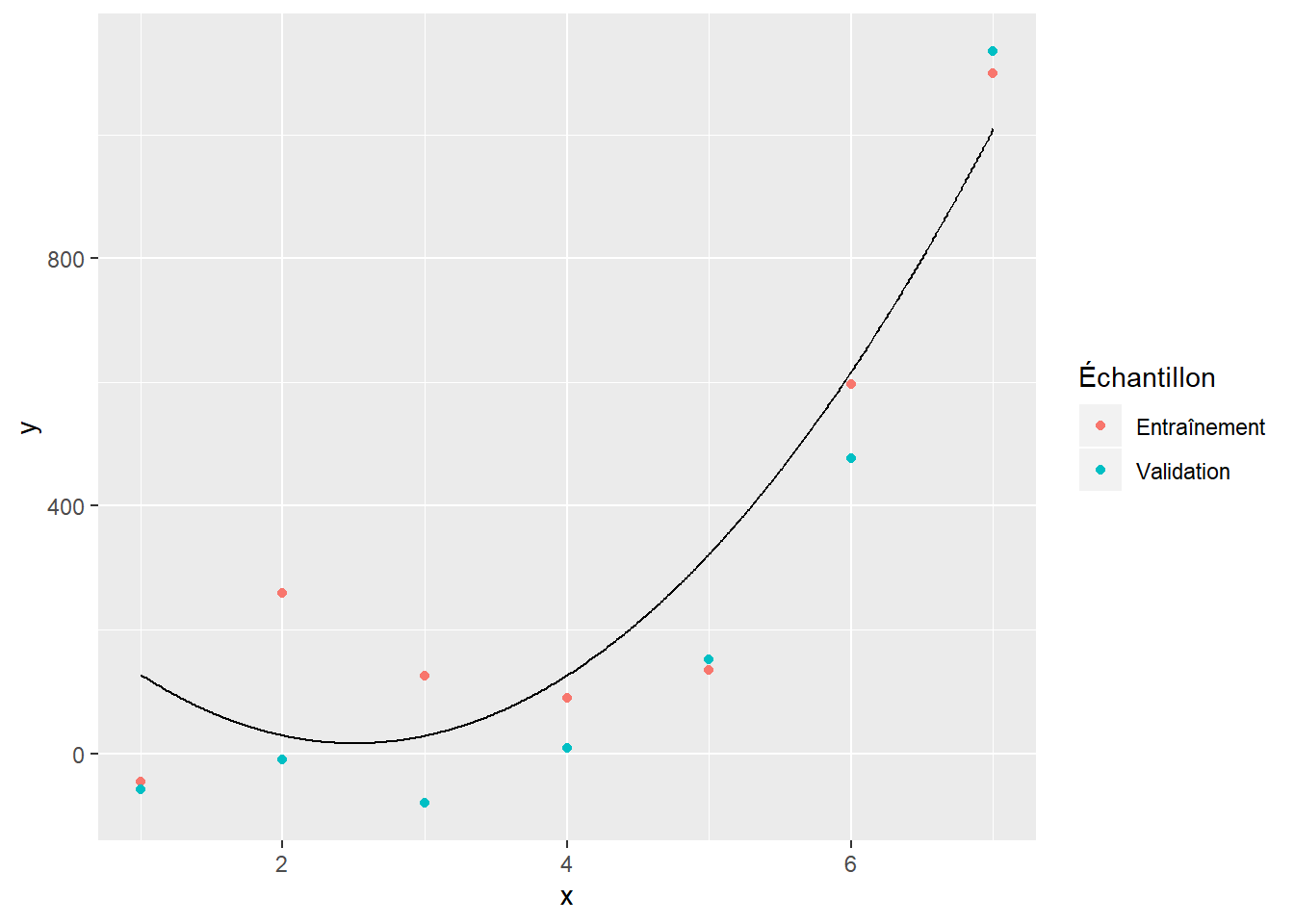
Figure 6.2: Polynôme d’ordre 2
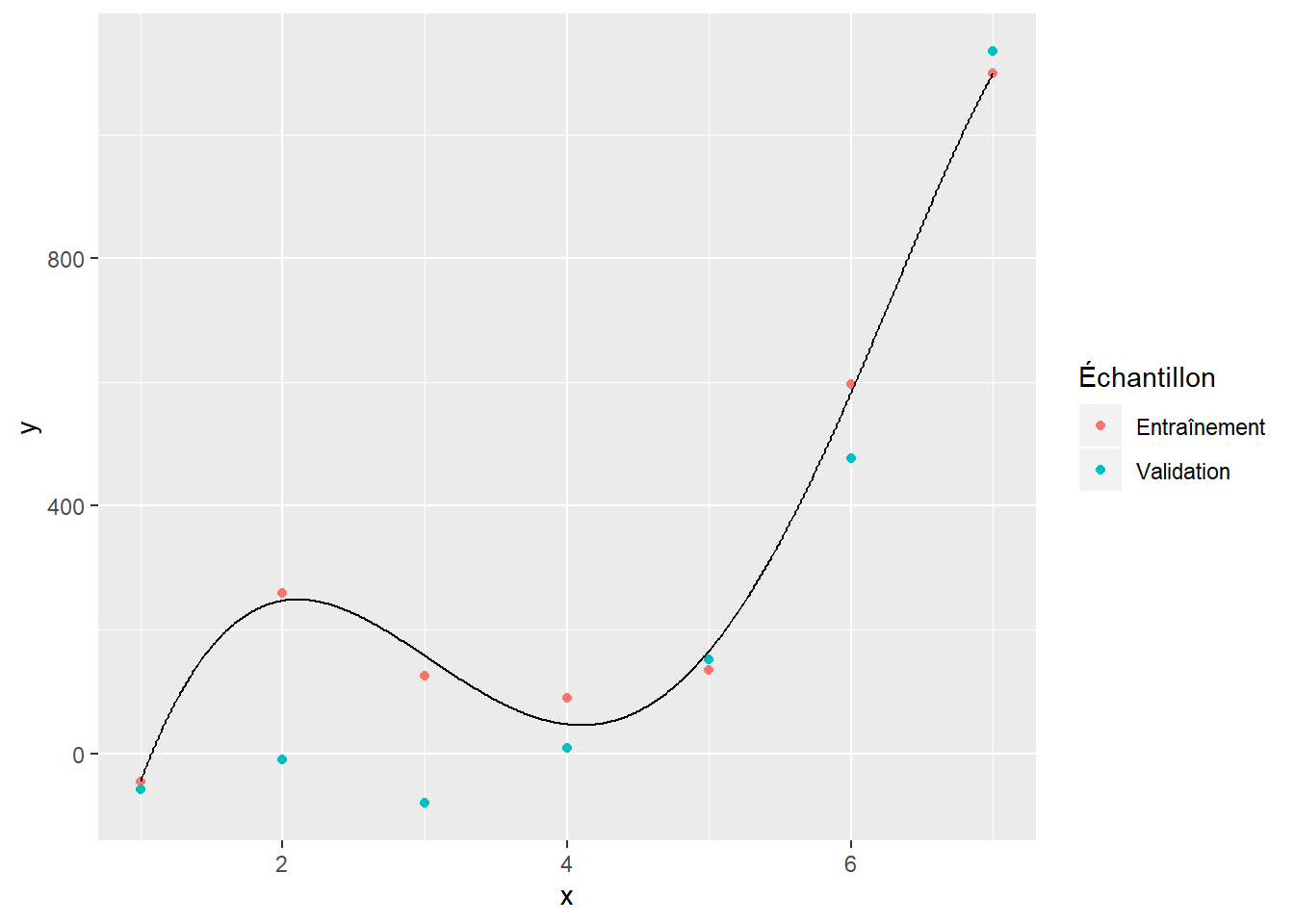
Figure 6.3: Polynôme d’ordre 5
De façon générale, les modèles trop complexes pour un jeu de données provoquent le phénomène de surapprentissage. La figure 6.4 est assez représentative du comportement de la performance d’un modèle en fonction de sa complexité. Ici, la comparaison se fait sur la base de la racine de l’erreur quadratique moyenne, mais il existe plusieurs autres critères de comparaison (voir section 6.4). L’interprétation de la figure 6.4 est la suivante:
- les polynômes d’ordre 0 et 1 donnent un modèle sousajusté (le modèle offre de piètres prédictions sur les deux jeux de données);
- les polynômes d’ordre 2 et 3 donnent de bons ajustements c’est-à dire qu’ils performent aussi bien (ou à peu près) sur les deux jeux de données;
- les polynômes d’ordre supérieur donnent un modèle surajusté, c’est-à-dire que leur performance est très bonne sur les données d’entraînement, mais plutôt mauvaise sur les données de validation. On remarque même une diminution de la performance sur l’échantillon de validation par rapport au polynôme d’ordre 2 et 3.
L’illustration du surajustement est présentée ici avec des polynômes, mais le même phénomène se produit avec toutes les catégories de modèles. Pour un arbre de classification, par exemple, l’augmentation de la complexité du modèle correspondrait à une augmentation de la profondeur de l’arbre. Pour un réseau de neurone, il pourrait par exemple s’agir d’ajouter des couches ou des neurones cachés.
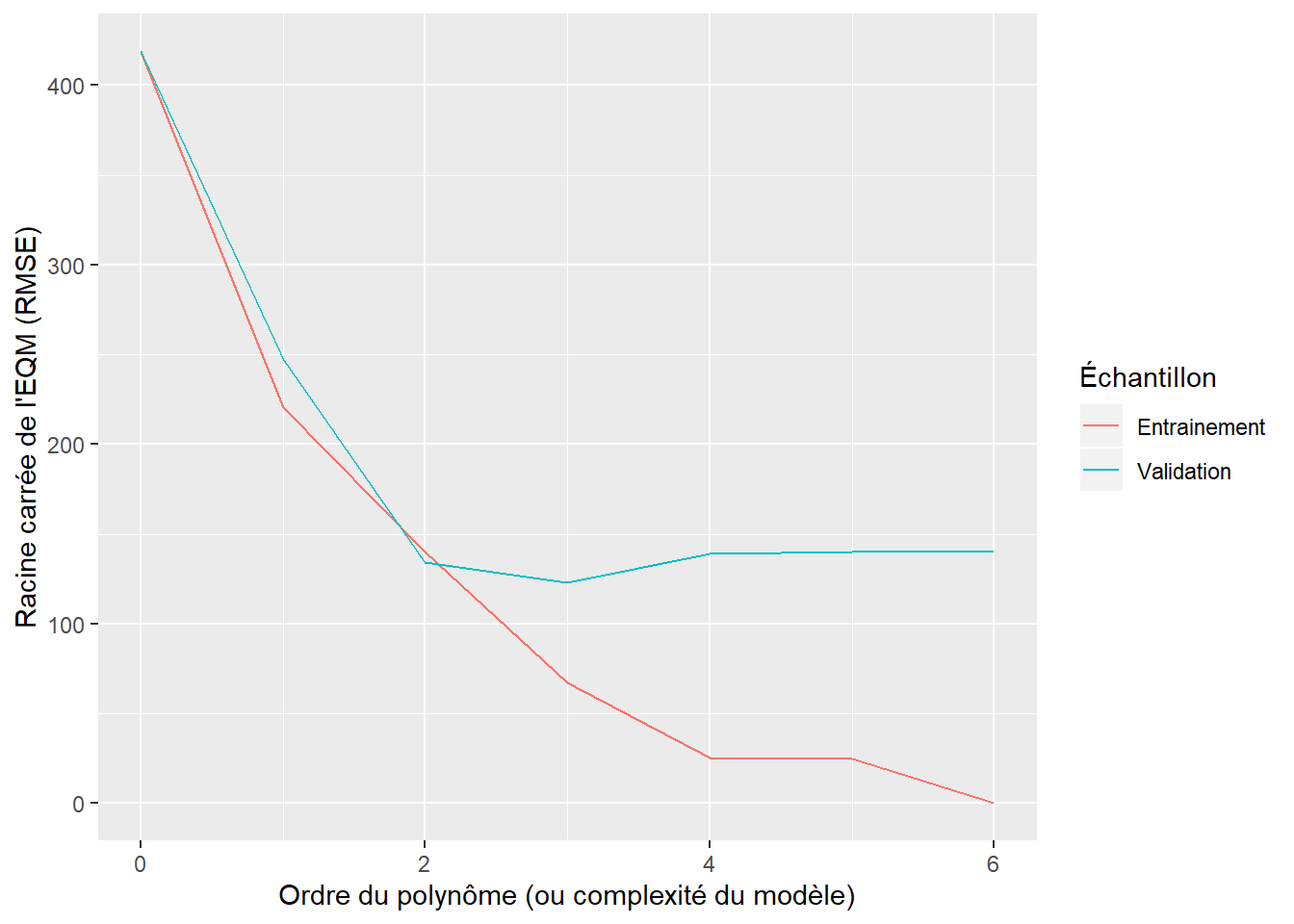
Figure 6.4: Performance du modèle en fonction de sa complexité
6.4 Critères de performance
Rappelons que les critères de performance doivent tous être calculés sur l’échantillon de validation pour éviter le problème de surajustement. Les sections suivantes présentent les principales mesures utilisées pour évaluer la performance.
Bien que ces mesures soient très faciles à calculer, il est plus pratique d’utiliser des fonctions pour les calculer. La librairie MLmetrics offre la majorité des mesures de performance intéressantes.
6.4.1 \(Y\) continue
Si \(Y\) est continue, on choisit généralement l’erreur quadratique moyenne comme critère de performance.
\[EQM = E\left[(y_i-\hat{y}_i)^2\right]\]
où \(y_i\) est la valeur de \(Y\) pour la \(i^e\) observation de l’échantillon de validation et \(\hat{y}_i\) est la prévision obtenue pour cette même observation avec le modèle créé lors de la phase d’entraînement.
Il y a toutefois des situations où l’on peut vouloir modifier cette mesure si l’on souhaite accorder plus d’importance à une partie des observations.
Avec la librairie MLmetrics, vous pouvez obtenir cette valeur avec la fonction MSE. On y préfère souvent la fonction RMSE qui fournit simplement la racine carrée de l’EQM.
6.4.2 \(Y\) binaire
En général, les modèles donnent une proportion \(\hat{p}_i\) pour chaque observation \(i\). On obtient une prévision en fixant un seuil \(s\) et on prédit
\[\hat{y}_i = 1 \text{ si } \hat{p}_i \geq s\] \[\hat{y}_i = 0 \text{ si } \hat{p}_i < s\]
Les mesures de performances des variables binaires seront illustrées à partir de l’exemple numérique suivant:
y_vrai <- c(1,0,1,0,1,0,1,0,1,0, 1,0,1,0,1,0,1,0,1,0)
y_predit <- c(1,1,1,0,0,0,1,0,1,1, 1,0,1,0,1,0,1,0,1,1)
y_proba <- c(0.9,0.55,0.65,0.32,0.35,0.25,0.52,0.45,0.84,0.65, 0.89,0.11,0.56,0.26,0.74,0.22,0.59,0.06,0.62,0.55)
don <- data.frame(y_vrai, y_proba, y_predit)| y_vrai | y_proba | y_predit |
|---|---|---|
| 1 | 0.90 | 1 |
| 0 | 0.55 | 1 |
| 1 | 0.65 | 1 |
| 0 | 0.32 | 0 |
| 1 | 0.35 | 0 |
| 0 | 0.25 | 0 |
| 1 | 0.52 | 1 |
| 0 | 0.45 | 0 |
| 1 | 0.84 | 1 |
| 0 | 0.65 | 1 |
| 1 | 0.89 | 1 |
| 0 | 0.11 | 0 |
| 1 | 0.56 | 1 |
| 0 | 0.26 | 0 |
| 1 | 0.74 | 1 |
| 0 | 0.22 | 0 |
| 1 | 0.59 | 1 |
| 0 | 0.06 | 0 |
| 1 | 0.62 | 1 |
| 0 | 0.55 | 1 |
Comparativement aux variables continues, il existe beaucoup plus de critères pour évaluer la performance d’un modèle avec une variable réponse binaire. La plupart s’appuient sur la matrice de confusion.
| \(\hat{y} = 0\) | \(\hat{y} = 1\) | |
|---|---|---|
| \(y = 0\) | Vrais négatifs (VN) | Faux positifs (FP) |
| \(y=1\) | Faux négatifs (FN) | Vrai positif (VP) |
En utilisant les données de l’exemple et en ajoutant les marges, on obtient:
# Matrice de confusion
confusion <- table(y_vrai,y_predit)
# Matrice de confusion avec les marges
confusion_marges <- addmargins(confusion)| y predit = 0 | y predit = 1 | Total | |
|---|---|---|---|
| y vrai = 0 | 7 | 3 | 10 |
| y vrai = 1 | 1 | 9 | 10 |
| Total | 8 | 12 | 20 |
La fonction ConfusionMatrix de la librairie MLmetrics permet d’obtenir la même matrice de confusion.
FALSE y_pred
FALSE y_true 0 1
FALSE 0 7 3
FALSE 1 1 9Le taux de bonne classification (et le taux d’erreur)
Le taux de bonne classification est la proportion des observations qui sont bien classées.
\[\frac{VN+VP}{VP+VN+FP+FN}=\mathbf{P}\left[(y=1 \cap \hat{y} = 1)\cup(y=0\cap\hat{y}=0)\right]\]
Pour l’exemple, on obtient un taux de bonne classification de \[\frac{7+9}{20} = 0.8\].
L’interprétation est que 80% des observations sont bien classées par le modèle.
Le taux d’erreur est la proportion des observations mal classées. On obtient: \[\frac{FN+FP}{N}=\frac{3+1}{20} = 0.2\]
La précision
La précision est la proportion de prévisions positives qui sont réellement positives.
\[\frac{VP}{VP+FP} = P(y=1|\hat{y}=1)\]
Dans l’exemple, on obtient
\[\frac{9}{3+9}= 0.75\]
Avec MLmetrics, on l’obtient avec la fonction Precision
# Calcul de la précision
precision <- Precision(y_pred = y_predit,
y_true = y_vrai,
positive = 1) # Attention, il faut spécifier la valeur qu'on considère comme étant positiveParmi les observations prédites positives, 75% sont réellement positives.
Sensibilité (rappel, recall)
C’est la proportion d’observations positives détectées par le modèle.
\[\frac{VP}{VP+FN} = P(\hat{y}=1|y=1)\]
Dans l’exemple,
\[\frac{9}{9+1} = 0.9\]
# Sensibilité
sensibilite <- Sensitivity(y_true = y_vrai,
y_pred = y_predit,
positive = 1)
# Rappel
sensibilite <- Recall(y_true = y_vrai,
y_pred = y_predit,
positive = 1)Le modèle détecte 90 % des cas où \(y = 1\).
Spécificité
C’est la proportion d’observations négatives détectées par le modèle.
\[\frac{VN}{VN+FP} = P(\hat{y}=0|y=0)\]
Dans l’exemple,
\[\frac{7}{7+3} = 0.7\]
Le modèle détecte 70 % des cas où \(y = 0\).
Score \(F_1\)
Les valeurs de précision, de sensibilité et de spécificité ne peuvent servir de mesure pour choisir le meilleur modèle, car on obtient des valeurs minimales ou maximales avec des modèles inutiles. Par exemple, on peut maximiser la sensibilité en prédisant toutes les valeurs à 1. Dans ce cas toutefois, la précision et le rappel seront nuls.
L’une des mesures utilisées pour combiner précision et sensibilité est le score \(F_1\):
\[F_1 = 2\frac{précision \times sensibilité}{précision + sensibilité}\]
Dans l’exemple,
\[F_1 = 2\frac{0.75 \times 0.9}{0.75+0.9}= 0.82\] En R, on l’obtient avec
Lors du choix du modèle, on souhaite un score le plus près possible de 1.
Le score F est une généralisation du score \(F_1\):
\[F = \frac{(1+\beta^2)précision \times sensibilité}{\beta^2 précision + sensibilité}\]
Le score \(F_1\) correspond au cas où \(\beta = 1\).
La courbe ROC et l’aire sous la courbe ROC
Jusqu’à maintenant, nous avons considéré un seul seuil \(s\) égal à \(0,5\), mais nous pourrions fixer ce seuil à n’importe quelle valeur entre 0 et 1 et calculer les mêmes mesures que précédemment.
Pour construire une courbe ROC, on calcule la sensibilité et la spécificité pour plusieurs seuils et on reporte ces valeurs sur un graphique dont l’axe des abscisses est 1-spécificité et l’axe des ordonnées est la sensibilité. Dans l’exemple, on obtient le graphique suivant:
# Construire une courbe ROC
# J'utilise la librairie pROC
library(pROC)
ROC <- roc(response = y_vrai,
predictor = y_proba)
ROC_dat <- data.frame(un_moins_specificite = rev(1 - ROC$specificities),
specificite = rev(ROC$specificities),
sensibilite = rev(ROC$sensitivities),
seuil = rev(ROC$thresholds))
courbe_roc <- ggplot(ROC_dat) +
geom_line(aes(un_moins_specificite,sensibilite, label = seuil))+
#geom_label(aes(un_moins_specificite,sensibilite, label = seuil))+
ylab('Sensibilite (taux de vrais positifs)')+
xlab('1-specificite (taux de faux positifs)')
ggplotly(courbe_roc, tooltip = c('seuil', 'sensibilite', 'un_moins_specificite'))Figure 6.5: Courbe ROC
Évidemment, on souhaite un modèle qui permet, pour certains seuils, d’atteindre à la fois une sensibilité de 1 et une spécificité de 1 (un taux de faux positifs de 0). Ainsi, un modèle parfait passerait par les points (0,1) et un mauvais modèle formerait une droite passant par les points (0,0) et (1,1) (voir la figure 6.6).
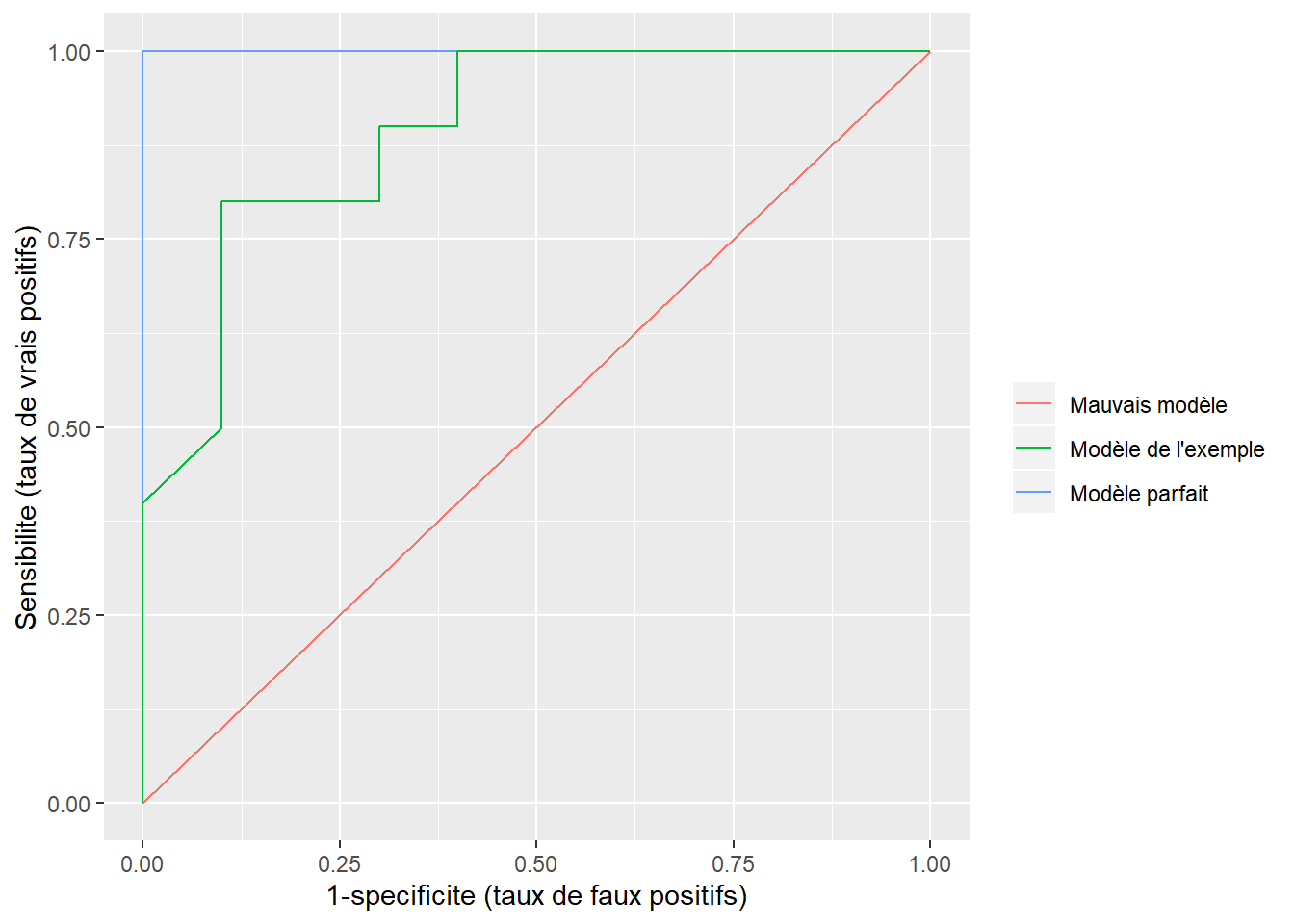
Figure 6.6: Comparaison des courbes ROC
Dans certains cas, la courbe ROC peut nous aider à choisir le seuil \(s\) au-delà duquel on considère que \(\hat{y}=1\). Pour comparer différents modèles entre eux, on utilisera plutôt l’aire sous la courbe. On l’obtient avec la fonction AUC de MLmetrics.
Taux de réponse, réponses capturées et levier
Le taux de réponse, les réponses capturées et le levier sont des mesures de sélection de modèles moins fréquemment utilisées que les mesures vues précédemment. Pour les calculer on classe les observations dans l’ordre décroissant de la probabilité prédite par le modèle et on sépare les observations classées en \(M\) groupes. Les statistiques sont calculées par groupe.
Dans l’exemple suivant, on a classé les 20 observations en ordre décroissant (avec arrange(desc(y_proba))) et on a regroupé les observations en \(M=5\) groupes (les groupes sont assignés avec mutate et le regroupement est fait avec group_by).
Pour chaque groupe, le taux de réponse est la proportion d’observations positives dans le groupe.
Pour le groupe 2, le taux de réponse cumulatif est la proportion des observations positives dans les groupes 1 et 2; pour le groupe 3, il s’agit de la proportion pour les groupes 1 à 3; et ainsi de suite.
taux_rep <- don %>%
arrange(desc(y_proba)) %>%
mutate(groupe = as.factor(rep(1:5, each = 4))) %>%
group_by(groupe)%>%
summarize( taille_groupe = 4, positif_obs = sum(y_vrai), taux_rep = positif_obs/4) %>%
mutate(taux_rep_cum = cumsum(positif_obs)/cumsum(taille_groupe))kable(taux_rep,
caption = 'Taux de réponse',
col.names = c('Nombre d\'observations dans le groupe', 'Groupe', 'Nombre d\'observations positives','Taux de réponse', 'Taux de réponse cumulé'))| Nombre d’observations dans le groupe | Groupe | Nombre d’observations positives | Taux de réponse | Taux de réponse cumulé |
|---|---|---|---|---|
| 1 | 4 | 4 | 1.00 | 1.000 |
| 2 | 4 | 3 | 0.75 | 0.875 |
| 3 | 4 | 2 | 0.50 | 0.750 |
| 4 | 4 | 1 | 0.25 | 0.625 |
| 5 | 4 | 0 | 0.00 | 0.500 |
Le taux de captures est la proportion des observations positives que nous parvenons à aller chercher dans un groupe. Dans l’exemple, le premier groupe, qui comprend les 20% d’observation dont les probabilités prédites sont les plus élevées, capture 40% des observations réellement positives.
Le taux de captures cumulé cumule simplement les observations positives capturées d’un groupe à l’autre. Dans le premier groupe, on avait capturé (détecté) 4 observations positives sur les 10. Le taux de réponses capturées est donc de 40%. Dans le second groupe, on en capture trois de plus. Le taux de réponse capturé passe à 70%.
nb_positifs_ech <- sum(don$y_vrai)
taux_rep_capt <- don %>%
arrange(desc(y_proba)) %>%
mutate(groupe = as.factor(rep(1:5, each = 4))) %>%
group_by(groupe) %>%
summarize(positif_obs = sum(y_vrai)) %>%
mutate(taux_capture = positif_obs/nb_positifs_ech, capture_cum = cumsum(positif_obs)/nb_positifs_ech)kable(taux_rep_capt,
caption = 'Taux de capture',
col.names = c('Groupe', 'Nombre d\'observations positives','Taux de capture', 'Taux de capture cumulé'))| Groupe | Nombre d’observations positives | Taux de capture | Taux de capture cumulé |
|---|---|---|---|
| 1 | 4 | 0.4 | 0.4 |
| 2 | 3 | 0.3 | 0.7 |
| 3 | 2 | 0.2 | 0.9 |
| 4 | 1 | 0.1 | 1.0 |
| 5 | 0 | 0.0 | 1.0 |
Le levier est le ratio entre le taux de réponse et la proportion des réponses positives dans l’ensemble groupe. Cette mesure s’apparente à celle de l’amélioration pour les règles d’association.
proportion_potitif_ech <- mean(don$y_vrai)
levier <- don %>%
arrange(desc(y_proba)) %>%
mutate(groupe = as.factor(rep(1:5, each = 4))) %>%
group_by(groupe)%>%
summarize(taux_rep = sum(y_vrai)/4) %>%
ungroup() %>%
mutate(levier = taux_rep/proportion_potitif_ech ) | Groupe | Taux de réponse | Levier |
|---|---|---|
| 1 | 1.00 | 2.0 |
| 2 | 0.75 | 1.5 |
| 3 | 0.50 | 1.0 |
| 4 | 0.25 | 0.5 |
| 5 | 0.00 | 0.0 |
Vous pouvez consulter la loi sur le site de l’Union européenne, mais l’article qui la vulgarise sur Wikipédia (https://fr.wikipedia.org/wiki/R%C3%A8glement_g%C3%A9n%C3%A9ral_sur_la_protection_des_donn%C3%A9es) est nettement plus accessible.↩︎
Le vocabulaire utilisé est similaire à celui utilisé par Hastie, Tibshirani, and Friedman (2009) et est probablement le plus répandu. L’ouvrage de Tufféry (2017) inverse le nom des deux dernières phases.↩︎