Chapitre 3 Analyse en composantes principales

Visualiser, comprendre, modéliser ou classifier des données sont toutes des tâches beaucoup plus simples à accomplir si le nombre de variables dans un jeu de données est faible. Si un jeu de données comprend un grand nombre de variables, une première question qu’on peut se poser est: est-il possible de réduire la dimension du problème sans trop perdre d’information?

En omettant tout simplement des variables, on risque de perdre beaucoup d’information utile. Une meilleure solution consiste à trouver des combinaisons linéaires des variables en vue de conserver le maximum d’information sur le jeu de données. C’est ce que l’on fera dans ce chapitre avec l’analyse en composante principale (ACP).

L’analyse en composantes principales (ACP) est une méthode qui permet de réduire la dimension d’un jeu de données tout en conservant le plus d’information possible. On l’utilise habituellement lorsqu’on a \(n\) observations de \(p\) variables continues et que \(p\) est trop grand pour nos besoins.

La méthode n’est pas particulièrement récente. Elle a été introduite par Pearson (1901) au début du XX\(^e\) siècle et a été formalisée par Hotelling (1933) dans un journal de psychologie quelques décennies plus tard. L’application présentée par Hotelling analysait les résultats des étudiants en lecture et en mathématique. Aujourd’hui, la méthode est utilisée dans une multitude d’applications où il est nécessaire de:

• visualiser un jeu de données de grande dimension;
• réduire le nombre de variables pour faciliter la construction de modèles (p.ex. en génétique ou en «text mining» , où \(p>>n\));
• faire une rotation d’axes pour simplifier la structure de corrélation;
• compresser des données.

Voici quelques exemples de situations où l’ACP peut être intéressante:

• comparer des équipes de hockey sur la base de 6 statistiques de fin de saison;
• comparer la criminalité entre états sur la base des taux de 7 types de crimes différents;
• compresser des images formées de \(1084\times1084\) pixels;
• identifier le nombre de variantes d’un type de tumeur à partir du degré d’expression de millions de gènes;
• analyser les réponses à un questionnaire sur la personnalité.

3.1 Mathématique de l’ACP

Globalement, lorsque l’on fait une ACP, on cherche une combinaison linéaire des variables qui maximise la variance, c’est-à-dire celle qui retient le maximum de l’information contenue dans le jeu de données. Les sections suivantes vous montrent comment on obtient ces combinaisons à l’aide des notions de valeurs et vecteurs propres (voir la section A.3 pour une révision de ces notions).

3.1.1 Calcul de la première composante principale

Soit un vecteur aléatoire composé de \(p\) variables \(\boldsymbol{X} = (X_1, \ldots , X_p)^\top\) ayant comme matrice de variance \(\text{var}(\boldsymbol{X})={\bf \Sigma}\) . On aimerait définir une première composante principale

\[ Y_1 = {\bf \alpha}_1^\top \boldsymbol{X} = \sum_{i=1}^p \alpha_{1i}X_i \]

de sorte que la variance de \(Y_1\) est maximale. L’idée est simple: on désire combiner \(p\) variables en une seule, mais en capturant la plus grande partie possible de la variabilité.

Technicalité: Il faut d’abord ajouter une contrainte sur \(\bf \alpha_1\), puisque sinon on n’aurait qu’à prendre des \(\alpha_{1i}\) qui sont égaux à \(\pm\infty\) et on aurait \(var(Y_1)=+\infty\), ce qui est définitivement maximal! On verra qu’il est pratique de contraindre \(\bf \alpha_1\) de sorte qu’il ait une norme égale à 1.

De la proposition B.1, on a que

\[{var}(Y_1) = {\bf \alpha}_1^\top \bf \Sigma \alpha_1.\]

Le problème est donc de maximiser

\[ F({\bf \alpha}_1) = {\bf \alpha}_1^\top {\bf \Sigma} {\bf \alpha}_1\]

sous la contrainte que \({\bf \alpha}_1^\top {\bf \alpha}_1 = 1\). On peut récrire ce problème à l’aide des multiplicateurs de Lagrange¹, soit maximiser

\[ F({\bf \alpha}_1, \lambda) = {\bf \alpha}_1^\top {\bf \Sigma} {\bf \alpha}_1 - \lambda ({\bf \alpha}_1^\top {\bf \alpha}_1 -1 )\]

où \(\lambda\) est un multiplicateur de Lagrange.

La solution du problème s’obtient en dérivant par rapport à \(\alpha_{11}\), \(\ldots\), \(\alpha_{1p}\) et \(\lambda\), ce qui assure que la contrainte \(||{\bf \alpha}_1|| =1\) est prise en compte, viz.

\[\frac{\partial}{\partial \lambda} \; F ({\bf \alpha}_1, \lambda) = 1-{\bf \alpha}_1^\top {\bf \alpha}_1 = 0. \]

Notons

\[\frac{\partial}{\partial {\bf \alpha}_1} \; F = \left( \frac{\partial}{\partial \alpha_{11}} \; F , \ldots , \frac{\partial}{\partial \alpha_{1p} } \; F \right)^\top .\]

En s’aidant de la proposition A.4, on obtient

\[\begin{equation} \frac{\partial}{\partial {\bf \alpha}_1} \; F ({\bf \alpha}_1, \lambda) = 2 {\bf \Sigma} {\bf \alpha}_1 - 2 \lambda {\bf \alpha}_1 = 0. \tag{3.1} \end{equation}\]

L’équation (3.1) est vraie si et seulement si \[\begin{equation} {\bf \Sigma} {\bf \alpha}_1 = \lambda {\bf \alpha}_1. \tag{3.2} \end{equation}\]

De la définition A.2, on déduit de (3.2) que

1. \({\bf \alpha}_1\) est un vecteur propre (normé) de \(\bf \Sigma\);
2. \(\lambda\) est la valeur propre correspondante.

Maintenant on a que \[{var} (Y_1) = {\bf \alpha}_1^\top {\bf \Sigma} {\bf \alpha}_1 = \lambda {\bf \alpha}_1^\top {\bf \alpha}_1 = \lambda. \] Puisque l’on veut maximiser cette quantité, on conclut que

1. \(\lambda = \lambda_1\), la plus grande valeur propre de \({\bf \Sigma}\);
2. \({\bf \alpha}_1\), le vecteur propre normé correspondant.

3.1.2 Calcul de la deuxième composante principale

On poursuit simultanément deux objectifs:

1. conserver le maximum de variation présente dans \({\bf {X}}\);
2. simplifier la structure de dépendance pour faciliter l’interprétation et assurer la stabilité numérique d’éventuelles méthodes qui utiliseront les composantes principales obtenues.

Étant donné \(Y_1\), la deuxième composante principale \(Y_2 = {\bf \alpha}_2^\top {\bf {X}}\) est définie telle que

1. \({var} (Y_2) = {\bf \alpha}_2^\top {\bf \Sigma} {\bf \alpha}_2\) est maximale;
2. \({\bf \alpha}_2^\top {\bf \alpha}_2 = 1\);
3. \(cov(Y_1,Y_2) = 0\).

On a que \[ \begin{eqnarray*} {\rm cov} (Y_1, Y_2) &=& {\rm cov} ({\bf \alpha}_1^\top \boldsymbol{X}, {\bf \alpha}_2^\top \boldsymbol{X}) \\ &=& {\bf \alpha}_1^\top {\bf \Sigma} {\bf \alpha}_2 = {\bf \alpha}_2^\top {\bf \Sigma} {\bf \alpha}_1 = \lambda_1 {\bf \alpha}_2^\top {\bf \alpha}_1. \end{eqnarray*} \]

On cherche donc le vecteur \({\bf \alpha}_2\) qui maximise \[ F({\bf \alpha}_2, \lambda, \kappa ) = {\bf \alpha}_2^\top {\bf \Sigma} {\bf \alpha}_2 - \lambda ({\bf \alpha}_2^\top {\bf \alpha}_2 - 1) - \kappa ({\bf \alpha}_2^\top {\bf \alpha}_1 - 0).\]

D’une part, \({\bf \alpha}_2\) est normé puisque \[\frac{\partial}{\partial \lambda} \; F ({\bf \alpha}_2, \lambda, \kappa ) = 1- {\bf \alpha}_2^\top {\bf \alpha}_2 = 0. \] D’autre part, \({\bf \alpha}_1\) et \({\bf \alpha}_2\) sont linéairement indépendants, car \[\frac{\partial}{\partial \kappa} \; F ({\bf \alpha}_2, \lambda, \kappa ) = - {\bf \alpha}_2^\top {\bf \alpha}_1 = -{\bf \alpha}_1^\top {\bf \alpha}_2 = 0. \]

Un calcul simple montre que \[\begin{equation} \frac{\partial}{\partial {\bf \alpha}_2} \; F ({\bf \alpha}_2, \lambda, \kappa ) = 2 {\bf \Sigma} {\bf \alpha}_2 - 2 \lambda {\bf \alpha}_2 - \kappa {\bf \alpha}_1 = 0. \tag{3.3} \end{equation}\]

En multipliant l’équation (3.3) à gauche et à droite par \({\bf \alpha}_1^\top\), on trouve

\[2{\bf \alpha}_1^\top {\bf \Sigma} {\bf \alpha}_2 - 2 {\bf \alpha}_1^\top \lambda {\bf \alpha}_2 - \kappa {\bf \alpha}_1^\top {\bf \alpha}_1 = 0. \] Mais \[{\bf \alpha}_1^\top {\bf \Sigma} = \lambda_1 {\bf \alpha}_1^\top, \; \; \; \mbox{et} \; \; \; {\bf \alpha}_1^\top {\bf \alpha}_1 = 1,\] d’où

\[ 2{\bf \alpha}_1^\top \lambda {\bf \alpha}_2 - 2 {\bf \alpha}_1^\top \lambda {\bf \alpha}_2 - \kappa {\bf \alpha}_1^\top {\bf \alpha}_1 = 0\implies - \kappa = 0. \] En substituant ce résultat dans (3.3), on obtient \[{\bf \Sigma} {\bf \alpha}_2 = \lambda {\bf \alpha}_2,\] et donc \(\lambda\) est une autre valeur propre de \({\bf \Sigma}\). Puisque \[{var} (Y_2) = {\bf \alpha}_2^\top {\bf \Sigma} {\bf \alpha}_2 = {\bf \alpha}_2^\top \lambda {\bf \alpha}_2 = \lambda, \] on a que cette variance est maximale si \(\lambda = \lambda_2\), la deuxième plus grande valeur propre de \({\bf \Sigma}\), et conséquemment \({\bf \alpha}_2\) est le vecteur propre normé correspondant.

3.1.3 Généralisation

En utilisant des maximisations successives, on conclut que \[\begin{eqnarray*} Y_k &= k^{\rm e} \mbox{ composante principale} \\ &= {\bf \alpha}_k^\top {\boldsymbol{X}}, \end{eqnarray*}\]

où \({\bf \alpha}_k\) est le vecteur propre normé associé à \(\lambda_k\), la \(k^{\rm e}\) plus grande valeur propre de \({\bf \Sigma}\).

3.1.4 Écriture matricielle

Pour définir simultanément et de façon plus compacte les composantes principales, et exprimer les composantes sous forme de colonne, comme nous avons l’habitude de les visualiser avec la plupart des logiciels, on pose

\[ {\bf {Y}} = {\boldsymbol{X}}{\bf {A}},\] où

\[{\bf {A}} = \left( {\bf \alpha}_1 , \ldots , {\bf \alpha}_p \right) = \left( \begin{array}{cccc} \alpha_{11} & \alpha_{21} & \cdots & \alpha_{p1} \\ \alpha_{12} & \alpha_{22} & \cdots & \alpha_{p2} \\ \vdots & \vdots & \vdots & \vdots \\ \alpha_{1p} & \alpha_{2p} & \cdots & \alpha_{pp} \end{array} \right). \]

Chaque colonne de \(\bf A\) est un vecteur propre de \(\Sigma\) et chaque colonne de \(\bf Y\) est une composante principale.

Proposition 3.1 Quelques propriétés en vrac de \(\bf{A}\).

• \(\bf{A}^\top \bf{A} = {\bf{A}\bf{A}}^\top = {\bf{I}}_p\);
• \({\bf{A}}^\top = {\bf{A}}^{-1}\).
• \({\bf \Sigma} {\bf{A}} = {\bf{A}}\bf{\Lambda}\), où \(\bf{\Lambda} = {\rm diag} (\lambda_1 , \ldots , \lambda_p)\).
• \({var} ({\bf{Y}}) = {\bf{A}}^\top {\bf \Sigma} {\bf{A}} = \bf{\Lambda}\Rightarrow\) \({cov} (Y_i, Y_j) = 0\) si \(i \neq j\) et \({var} (Y_i) = \lambda_i \ge {var} (Y_j) = \lambda_j\) si et seulement si \(i \le j\).

3.1.5 Variation expliquée

La trace de Pillai est une mesure globale de la variation: \[\begin{equation} {\rm tr} ({\bf \Sigma}) = {\rm tr} (\bf{\Lambda}) = \sum_{i=1}^p\lambda_i. \tag{3.4} \end{equation}\]

La proportion de variation expliquée la composante principale \(Y_i\) est \[\frac{\lambda_i}{\lambda_1 + \cdots + \lambda_p} .\]

3.2 Exemple de calcul

Exemple 3.1 L’exemple de calcul se fera sur un échantillon de données climatiques provenant du site web d’Environnement Canada. On analysera les variables climatiques (température maximale moyenne et précipitations totales) de certaines stations météo canadiennes pour les mois de mars, juin, septembre et décembre 2010.

3.2.1 Standardisation

L’ACP est une technique très sensible à l’échelle de mesure des variables. En effet, puisque l’ACP cherche une combinaison qui maximise la variance, une variable \(X_i\) de grande variance aura un poids démesuré dans les composantes principales. Par exemple la mesure la distance en mètres plutôt qu’en kilomètres multiplierait la variance de cette variable par un million et elle aurait un poids majeur dans toutes les composantes. C’est pourquoi on recommande très fortement d’effectuer l’ACP sur les variables standardisées, à moins qu’elles n’aient déjà des variances plutôt similaires. On notera le vecteur aléatoire standardisé \(X^*\).

# Standardiser X
X <- scale(as.matrix(climat[,6:13]))

# Nombre d'observations
n <- nrow(X)

# Nombre de variables 
p <- ncol(X)

3.2.2 Estimation de \(\Sigma\)

En général, la valeur de \(\Sigma\) n’est pas connue. Comme on l’a vu à la section B.2, à partir d’un échantillon aléatoire \({X}_1, \ldots , {X}_n\), elle peut être estimée par la matrice de variance-covariance. \[ \begin{eqnarray*} \boldsymbol{S}^2 &=& \frac{1}{n-1} \, \sum_{i=1}^n \left( {\boldsymbol{X^*}}_i - {\bar {\boldsymbol{X^*}}} \right)^\top \left( {\boldsymbol{X^*}}_i - {\bar {\boldsymbol{X^*}}} \right)\\ &=& \frac{1}{n-1} X^{*\top}X^* \end{eqnarray*} \]

# Calculer la matrice de variance-covariance estimée
S2 <- (t(X) %*% X) / (n - 1)

#S2 <- cov(X) # Vous donnerait le même résultat

3.2.3 Calcul des vecteurs propres de \(S^2\) (\(\bf A\))

\({\boldsymbol{S}^2}\) est une matrice carrée symétrique. Règle générale, \({\boldsymbol{S}^2}\) est inversible; elle l’est avec probabilité si \({\boldsymbol{X}} \sim {N}_p (\bf{\mu}, \bf{\Sigma})\) (sous certaines conditions mineures pour \(\bf{\Sigma}\)).

Elle admet alors la représentation \[\boldsymbol{S}^2 = {\hat {\bf{A}}} {\bf{L}} {\hat {\bf{A}}}^\top,\] où \({\hat {\bf{A}}} = (a_{ij})\) et \({\bf{L}} = {\rm diag} (\lambda_1, \ldots ,\lambda_p)\).

Autrement dit, cette matrice se décompose en valeurs propres.

# Calculer les vecteurs propres
vp <- eigen(S2)

# Transformer les vecteurs propres en matrice
A <- as.matrix(vp$vectors)

# Extraire les vecteurs propres (3 premières valeurs des 3 premiers vecteurs)
A[1:3,1:3]

FALSE            [,1]      [,2]        [,3]
FALSE [1,] -0.4069811 0.3349289 -0.12299842
FALSE [2,] -0.3476355 0.4837931 -0.08871299
FALSE [3,] -0.4558086 0.2266724  0.08910420

# Extraire les valeurs propres
lambda <- vp$values

3.2.4 Calcul des composantes principales (\(Y\))

Il ne reste qu’à calculer les composantes principales \({\bf {Y}} = \boldsymbol{X}^* {\bf {A}}\).

# Calculer les composantes principales
Y <- X %*% A

# Extraire les composantes principales (3 premières valeurs des 3 premières composantes)
Y[1:3,1:3]

FALSE           [,1]      [,2]      [,3]
FALSE [1,] -1.176005 -1.272778 -1.177800
FALSE [2,] -1.580160 -3.291723 -0.677234
FALSE [3,] -2.415575 -5.041825 -1.305001

Notez que si \(\lambda_1 > \cdots > \lambda_p\), alors les composantes principales sont uniques, à un signe près.

Chaque colonne de \(\bf Y\) présente une composante principale. Dans l’exemple, \(\bf Y\) a donc 189 ligne et 8 colonne.

3.2.5 Calcul de la proportion de la variation expliquée

Rappelons que la proportion de variation expliquée la composante principale \(Y_i\) est \[\frac{\lambda_i}{\lambda_1 + \cdots + \lambda_p} .\]

On s’intéressera à la proportion de la variance de chaque composante, mais aussi à la somme cumulée de la variance expliquée par les premières composantes (voir tableau 3.1).

# Calculer la proportion de la variation expliquée
prop_var <- vp$values / sum(vp$values)
# Faire la somme cumulée de la proportion de la variation expliquée
prop_var_cum <- cumsum(vp$values / sum(vp$values))

kable(data.frame(prop_var = round(prop_var,2),
                 prop_var_cum = round(prop_var_cum,2)),
      caption = 'Proportion de la variation expliquée')

Tableau 3.1: Proportion de la variation expliquée

prop_var	prop_var_cum
0.51	0.51
0.22	0.73
0.10	0.82
0.08	0.90
0.05	0.95
0.03	0.98
0.01	0.99
0.01	1.00

3.3 En pratique

3.3.1 Les fonctions pour faire l’ACP en R

Bien que le calcul des composantes principales soit relativement facile, on préférera souvent utiliser des fonctions qui facilitent le travail. En R, il existe deux fonctions dans la librairie de base stats pour faire l’ACP: princomp et prcomp

Fonctions de base

La fonction princomp calcule les composantes principales comme exposé dans la section précédente, à la différence qu’elle utilise un estimateur biaisé de la matrice de variance-covariance (B.1). En précisant l’argument cor=TRUE, les composantes sont calculées à partir de la matrice de corrélation, ce qui revient à travailler sur les données standardisées.

# Calculer les composantes principales
acp_princomp <- princomp(scale(climat[,6:13]),
                         cor = TRUE) # Utiliser les données standardisées

# Extraire les composantes principales (3 premières valeurs des 3 premières composantes)
acp_princomp$scores[1:3,1:3]

FALSE        Comp.1    Comp.2    Comp.3
FALSE [1,] 1.179128 -1.276159 1.1809285
FALSE [2,] 1.584357 -3.300466 0.6790328
FALSE [3,] 2.421991 -5.055216 1.3084668

# Extraire les vecteurs propres (3 premières valeurs des 3 premiers vecteurs)
acp_princomp$loadings[1:3,1:3]

FALSE              Comp.1    Comp.2      Comp.3
FALSE tmax_mars 0.4069811 0.3349289  0.12299842
FALSE tmax_juin 0.3476355 0.4837931  0.08871299
FALSE tmax_sept 0.4558086 0.2266724 -0.08910420

La fonction prcompoffre l’avantage d’une plus grande stabilité numérique. Plutôt que de calculer les valeurs propres, cette fonction utilise la décomposition en valeur singulière (voir section A.4). De plus, elle utilise l’estimateur non biaisé de la matrice de variance-covariance (B.2). Pour travailler sur les données standardisées, il faut spécifier center = TRUE et scale = TRUE.

# Calculer les composantes principales
acp_prcomp <- prcomp(scale(climat[,6:13]),
                     center = TRUE, scale = TRUE)# Important pour travailler sur les données standardisées 

# Extraire les composantes principales (3 premières valeurs des 3 premières composantes)
acp_prcomp$x[1:3,1:3]

FALSE            PC1       PC2       PC3
FALSE [1,] -1.176005 -1.272778 -1.177800
FALSE [2,] -1.580160 -3.291723 -0.677234
FALSE [3,] -2.415575 -5.041825 -1.305001

# Extraire les vecteurs propres (3 premières valeurs des 3 premiers vecteurs)
acp_prcomp$rotation[1:3,1:3]

FALSE                  PC1       PC2         PC3
FALSE tmax_mars -0.4069811 0.3349289 -0.12299842
FALSE tmax_juin -0.3476355 0.4837931 -0.08871299
FALSE tmax_sept -0.4558086 0.2266724  0.08910420

Librairie FactoMineR

Enfin, la librairie la plus complète en R pour faire ce type d’analyse est FactoMineR (Lê, Josse, and Husson (2008)). La fonction pour faire l’ACP est PCA. Par défaut, cette fonction standardise les variables. Pour la suite, nous nous en tiendrons à cette librairie.

# Faire l'ACP
climat_pca <- PCA(climat[6:13], 
                  ncp = 8,
                  graph = FALSE)

# Extraire les composantes principales (3 premières valeurs des 3 premières composantes)
climat_pca$ind$coord[1:3,1:3]

FALSE      Dim.1    Dim.2      Dim.3
FALSE 1 1.179128 1.276159 -1.1809285
FALSE 2 1.584357 3.300466 -0.6790328
FALSE 3 2.421991 5.055216 -1.3084668

# Extraire les vecteurs propres
climat_pca$svd$V[1:3,1:3]

FALSE           [,1]       [,2]        [,3]
FALSE [1,] 0.4069811 -0.3349289 -0.12299842
FALSE [2,] 0.3476355 -0.4837931 -0.08871299
FALSE [3,] 0.4558086 -0.2266724  0.08910420

3.3.2 Interprétation des poids

On cherche généralement à trouver une signification aux coordonnées dans les premières composantes principales en regardant les poids \(\alpha_{ij}\) accordés aux variables originales dans les composantes principales.

Quand on parle des poids des composantes principales, on fait référence aux vecteurs propres de \(\boldsymbol{S}^2\). Dans l’exemple 3.1, le premier vecteur propre est

# Extraire les vecteurs propres (3 premières valeurs des 3 premiers vecteurs)
poids <- climat_pca$svd$V
row.names(poids) <- colnames(climat[6:13])
colnames(poids) <- paste0('CP', c(1:8))
alpha1 <- round(poids[,1],2)
alpha1

FALSE   tmax_mars   tmax_juin   tmax_sept    tmax_dec precip_mars precip_juin 
FALSE        0.41        0.35        0.46        0.39        0.27        0.32 
FALSE precip_sept  precip_dec 
FALSE        0.33        0.26

La première composante est donc donnée par \(Y_1 =\) 0.41 \(\times\) tmax_mars \(+\) 0.35 \(\times\) tmax_juin $+$0.46 \(\times\) tmax_sept $+$0.39 \(\times\) tmax_dec $+$0.27 \(\times\) precip_mars $+$0.32 \(\times\) precip_juin $+$0.33 \(\times\) precip_sept $+$0.26 \(\times\) precip_dec.

Pour interpréter les poids des composantes, le plus simple est souvent de les trier ou de les présenter sous la forme d’un tableau interactif.

# Afficher les poids dans un tableau interactif
datatable(round(poids[,1:5],2),
           options = list(dom = 't'))

Figure 3.1: Poids (vecteurs propres)

En triant le tableau précédent (3.1), on remarque que les villes qui ont une valeur très élevée sur la première composante sont celles où les températures maximales sont très élevées, particulièrement en septembre et en mars. Les précipitations y seront plutôt élevées, mais cet aspect est moins important pour cette composante que la température. La première composante oppose donc les températures froides aux températures plus élevées. Cette interprétation devient évidente lorsque l’on visualise le tout sur une carte (figure 3.2).

Sur la deuxième composante, les villes aux scores élevés sont celles dont la température est basse en juin et en mars et le climat humide en mars et en décembre.

Dans l’interprétation des composantes, on s’en tient généralement aux poids les plus grands en valeur absolue. Les sections 3.3.3 et 3.3.4 vous fourniront plus d’outils pour l’interprétation des axes.

Dans l’exemple 3.1, la carte est une représentation naturelle des données. En visualisant les deux premières composantes sur une carte géographique, on constate très facilement que la première composante est liée à la température. La deuxième composante parait plus manifestement liée aux précipitations.

# On ajoute les autres informations sur les stations, incluant les coordonnées géographiques
climat_acp <- cbind(climat, climat_pca$ind$coord)

# Faire une présentation géographique des composantes principales
pal1 <- colorNumeric(
  palette = "RdYlBu",
  domain = climat_acp$Dim.1,
  reverse = TRUE)
pal2 <- colorNumeric(
  palette = "RdYlBu",
  domain = climat_acp$Dim.2,
  reverse = TRUE)

leaflet(climat_acp) %>% 
  addTiles() %>%
  #addProviderTiles(providers$CartoDB.Positron) %>%
  addCircleMarkers(lng = ~longitude, 
             lat = ~latitude, 
             color = ~pal1(Dim.1),
             radius = 2,
             opacity = 1, 
             fill = TRUE, 
             fillColor = ~pal1(Dim.1), 
             fillOpacity = 1,
             group = 'Composante 1'
             ) %>%
  addCircleMarkers(lng = ~longitude, 
             lat = ~latitude, 
             color = ~pal2(Dim.2),
             radius = 2,
             opacity = 1, 
             fill = TRUE, 
             fillColor = ~pal2(Dim.2), 
             fillOpacity = 1,
             group = 'Composante 2'
             ) %>%
  addLegend("bottomright", pal = pal1, values = ~Dim.1,
    title = "CP1",
    opacity = 1,
    group = 'Composante 1'
    ) %>%
  addLegend("bottomleft", pal = pal2, values = ~Dim.2,
    title = "CP2",
    opacity = 1,
    group = 'Composante 2'
    ) %>%
  addLayersControl(
    baseGroups = c("Composante 1", "Composante 2"),
    options = layersControlOptions(collapsed = FALSE)
  )

Figure 3.2: Représentation géographique de l’ACP

3.3.3 Analyse des observations (individus)

3.3.3.1 Représentation graphique des observations

D’un point de vue géométrique, l’ACP projette les observations dans un sous-espace de dimensions inférieur et les composantes principales calculées précédemment sont simplement les coordonnées des observations sur les nouveaux axes, qu’on nomme parfois axes factoriels.

En effet, puisque \({\bf A}\) est orthonormale, \({\bf {Y}} = \boldsymbol{X}^* {\bf {A}}\) représente une rotation d’axes. Les nouveaux axes correspondent aux directions orthogonales de variation maximale successives (en supposant toujours \(\lambda_1 > \cdots > \lambda_p\)).

La formule \[ {\bf {Y}} = \boldsymbol{X}^* {\bf {A}}\] donne donc les coordonnées de l’observation \({{\boldsymbol X}}_i\) dans le nouveau système d’axes.

La fonction PCA offre une option pour visualiser les coordonnées des observations (les stations de l’exemple 3.1) sur les deux premiers axes, mais le résultat n’est pas très joli et n’aide pas beaucoup à l’interprétation (voir la figure 3.3).

# Afficher le graphique par défaut pour les individus
plot.PCA(climat_pca, axes = c(1,2), choix = 'ind')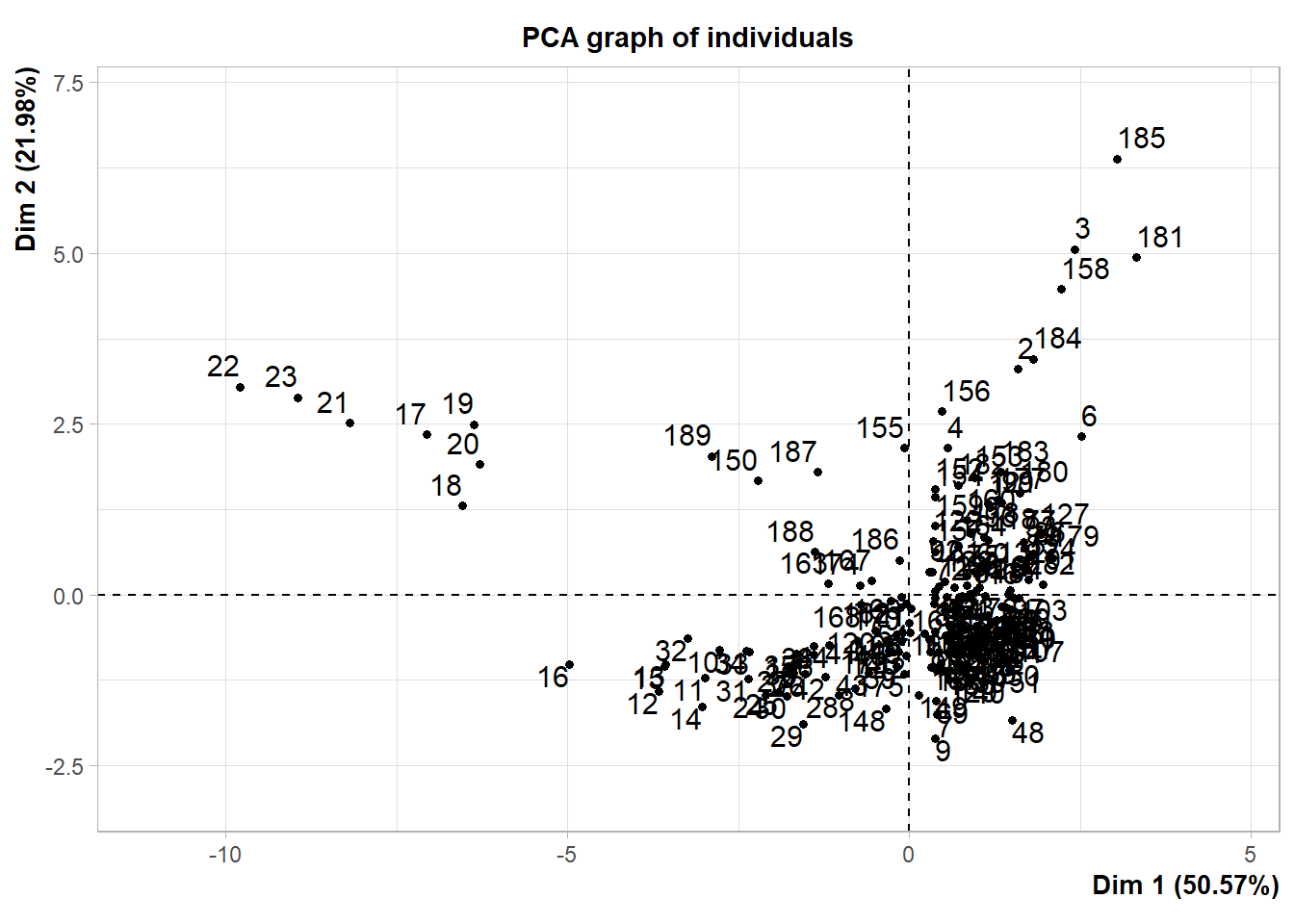

Figure 3.3: Représentation par défaut de l’ACP

Pour faciliter l’interprétation, il faudra faire preuve d’un peu plus d’ingéniosité et utiliser les graphiques interactifs. Dans cet exemple, l’ACP sera beaucoup plus facile à visualiser avec des couleurs pour distinguer les provinces. Comme notre cerveau a de la difficulté à traiter l’information de 13 couleurs différentes, regroupons d’abord les provinces en cinq régions.

# Créer des groupes de provinces pour faciliter la visualisation
climat_acp <- climat_acp %>%
  mutate(region = case_when(
    province %in% c('ALBERTA', 'SASKATCHEWAN') ~ "AB et SK",
    province %in% c('BRITISH COLUMBIA') ~ "BC",
    province %in% c('ONTARIO', 'MANITOBA', 'QUEBEC') ~ "Centre",
    province %in% c("NOVA SCOTIA" , "PRINCE EDWARD ISLAND","NEWFOUNDLAND","NEW BRUNSWICK") ~ "Maritimes",
    province %in% c("YUKON TERRITORY"   , "NORTHWEST TERRITORIES","NUNAVUT") ~ "Nord"
  ))

On peut ensuite illustrer les deux premières composantes avec un graphique interactif. Sur la figure 3.4, on voit que les régions très froides de septembre à mars se distinguent sur l’axe de la première composante. La seconde composante permet d’identifier les régions maritimes (dans les valeurs élevées) et les régions aux températures plus chaudes de mars à septembre (dans les valeurs faibles).

# Faire un graphique des individus projetés dans les axes factoriels
g_ind <- ggplot() +
  geom_point(data = climat_acp, 
             aes(Dim.1, Dim.2, colour = region, label = location)) +
  ylab('CP2') +
  xlab('CP1')  +
  theme_minimal() 

# Rendre le graphique interactif avec plotly
ggplotly(g_ind, tooltip = 'location')

Figure 3.4: Projection des villes canadiennes dans les dimensions des composantes principales

3.3.3.2 Contribution de chaque observation aux composantes

Rappelons que chaque composante principale capture une partie de la variabilité totale des données. La variance associée à la \(k^{ième}\) composante est \(\lambda_k\). Chaque individu du jeu de données contribue à la variabilité présente dans chaque composante. On peut mesurer la contribution de l’individu \(i\) à la composante \(k\) de la façon suivante:

\[C^{(obs)}_{i,k}= \frac{Y_{i,k}^2/n}{\lambda_k}\]

où \(Y_{i,k}\) est la coorodnnée de l’individu \(i\) sur l’axe factoriel \(k\) et \(n\) est la taille de l’échantillon.

Voici un exemple de calcul pour le premier individu:

# Calculer la contribution de l'individu 1 à la composante 1
contribi1 <- climat_pca$ind$coord[1,1]^2/n/climat_pca$eig[1,1]*100

Ceci signifie que le premier individu contribue pour 0.18 % de la variance de la première composante principale. Cette mesure peut être utile dans l’interprétation des axes: on essairea d’interpréter les axes en regardant plus en détails les individus qui ont une forte contribution sur chaque axe. On pourrait aussi utiliser cette mesure pour éviter les cas où un seul individu défini à lui seul la majorité de la variabilité d’un axe.

On trouve aussi cette valeur dans la sortie de PCA:

# Afficher la contribution des trois premiers individus sur les 3 premiers axes
climat_pca$ind$contrib[1:3,1:3]

FALSE       Dim.1    Dim.2     Dim.3
FALSE 1 0.1818214 0.490047 0.9638561
FALSE 2 0.3282687 3.277772 0.3186739
FALSE 3 0.7671286 7.689669 1.1832879

3.3.3.3 Qualité de la représentation d’une observation sur chaque composante

La qualité de la représentation indique à quel point l’individu est bien représenté par cet axe. Pour obtenir cette mesure, on calcule d’abord la distance \(d_i\) d’une observation par rapport à l’origine (dans l’espace des axes factoriels)

\[d_i = \sqrt{\sum_{k=1}^p Y_{i,k}^2}\]

où \(p\) est le nombre de variables.

# Calculer la distance de l'individu 1 par rapport à l'origine
d1 <- sqrt(sum(climat_pca$ind$coord[1,]^2))

La qualité de la représentation sur l’axe \(k\) s’obtient par

\[Q^{(obs)}_{i,k} = \frac{Y_{i,k}^2}{d_i^2}\]

# Calculer la qualité de l'individu 1 sur le premier axe
q1 <- climat_pca$ind$coord[1,1]^2 / d1^2
q1

FALSE [1] 0.1141067

On trouve aussi cette valeur dans la sortie de PCA:

# Qualité des trois premiers individus sur les deux premiers axes
climat_pca$ind$cos2[1:3, 1:2]

FALSE        Dim.1     Dim.2
FALSE 1 0.11410672 0.1336592
FALSE 2 0.09629467 0.4178750
FALSE 3 0.15030426 0.6547955

3.3.4 Analyse des variables

3.3.4.1 Représentation graphique des variables

Pour illustrer les variables dans l’ACP, on présente généralement un graphique similaire à celui de la figure 3.5. La coordonnée de la première variable sur l’axe des abscisses correspond à la corrélation entre cette variable et la première composante principale; la coordonnée sur le second axe correspond à la corrélation entre cette variable et la seconde composante principale; et ainsi de suite. De façon plus générale, on obtient la corrélation entre chaque variable et chaque composante par

\[ {\bf R} = cor(X,Y)\]

où \(r_{j,k}\) est la coordonnée de la variable \(j\) sur l’axe de la \(k^{ème}\) composante, c’est-à-dire la corrélation entre la \(j^{ème}\) variable et la \(k^{ème}\) composante principale.

Voici un exemple de calcul:

# Calcul des coordonnées des variables (corrélation avec les axes)
coord_var <- cor(X,Y) 
coord_var[1:3,1:2]

FALSE                 [,1]      [,2]
FALSE tmax_mars -0.8186190 0.4441275
FALSE tmax_juin -0.6992487 0.6415265
FALSE tmax_sept -0.9168327 0.3005755

#coord_var <- A %*% diag(sqrt(lambda)) # Donne le même résultat
#coord_var <- t(X) %*% (scale(Y)) / (n-1) # Donne le même résultat

On trouve ces valeurs facilement dans la sortie de PCA:

# Extraire les trois premières coordonnées des deux premières variables 
climat_pca$var$coord[1:3,1:2]

FALSE               Dim.1      Dim.2
FALSE tmax_mars 0.8186190 -0.4441275
FALSE tmax_juin 0.6992487 -0.6415265
FALSE tmax_sept 0.9168327 -0.3005755

On obtient aussi un graphique par défaut avec la fonction plotPCA.

# Afficher le graphique par défaut des variables
plot.PCA(climat_pca, 
         axes = c(1,2), 
         choix = 'var')

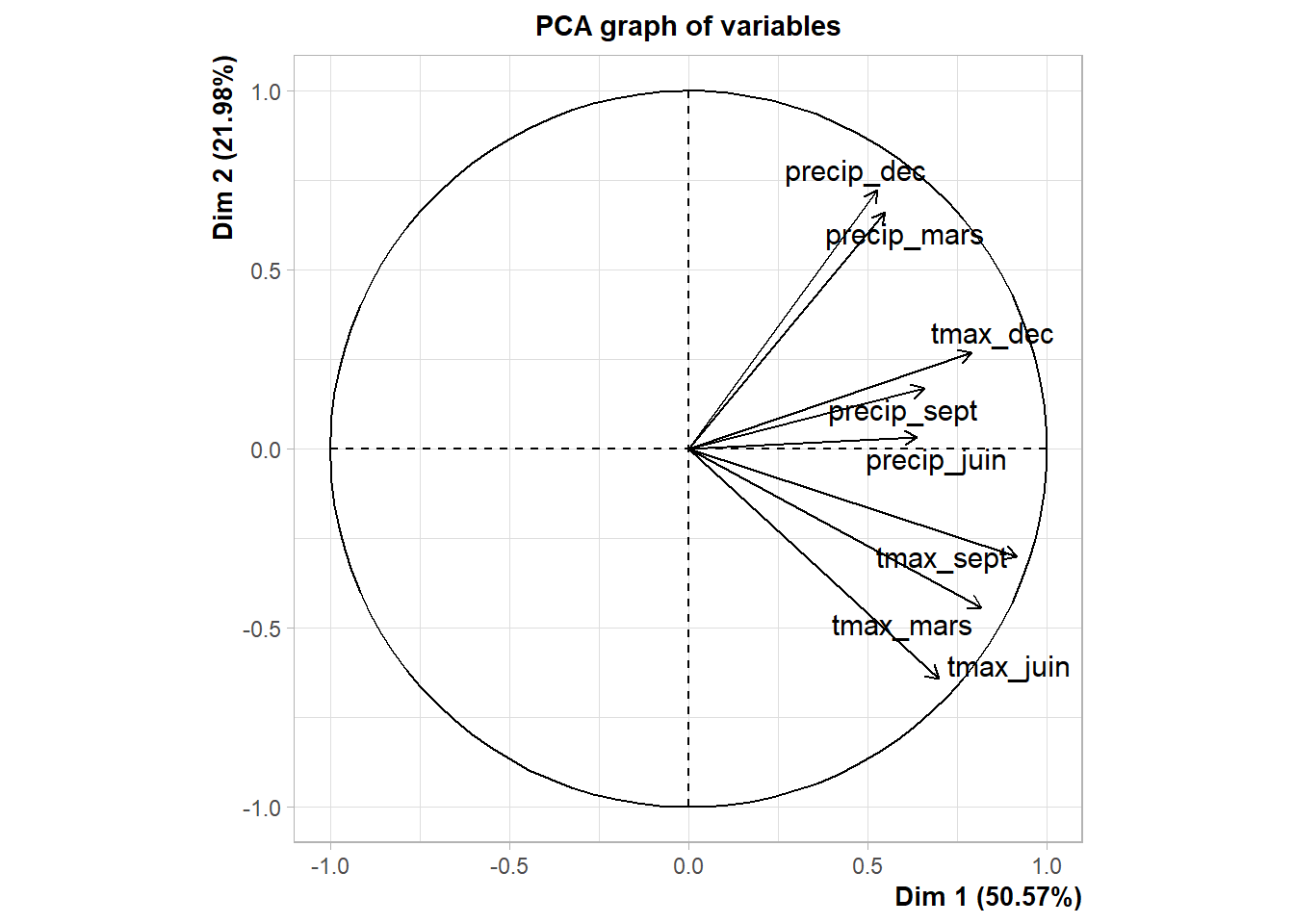
Figure 3.5: Représentation par défaut des variables sur les premiers axes de l’ACP

Encore une fois, le graphique n’est pas très joli. On peut l’améliorer un peu.

# Améliorer le graphique des variables

# Mettre les coordonnées dans un dataframe
corr_dt <- as.data.frame(climat_pca$var$coord)
noms_var <- rownames(corr_dt)

# Tracer le cercle
tt <- seq(0,2*pi,length.out = 100)
cercle <- data.frame(x = cos(tt), y = sin(tt))

# Présenter les variables et le cercle sur une même figure
g_var <- ggplot() +
  geom_text(data = corr_dt, 
            aes(x = Dim.1, y = Dim.2, label = noms_var),  
            hjust = 'left', 
            vjust = 'middle') +
  xlim(c(-1.2,1.2)) +
  ylim(c(-1.2,1.2)) +
  geom_segment(data = corr_dt, 
               aes(x = 0, y = 0, xend = Dim.1, yend = Dim.2),  
               arrow = arrow(length = unit(0.2,"cm"), type = 'closed')
               ) +
  geom_polygon(data = cercle, aes(x,y), alpha = 0.1) +
  theme_minimal()

g_var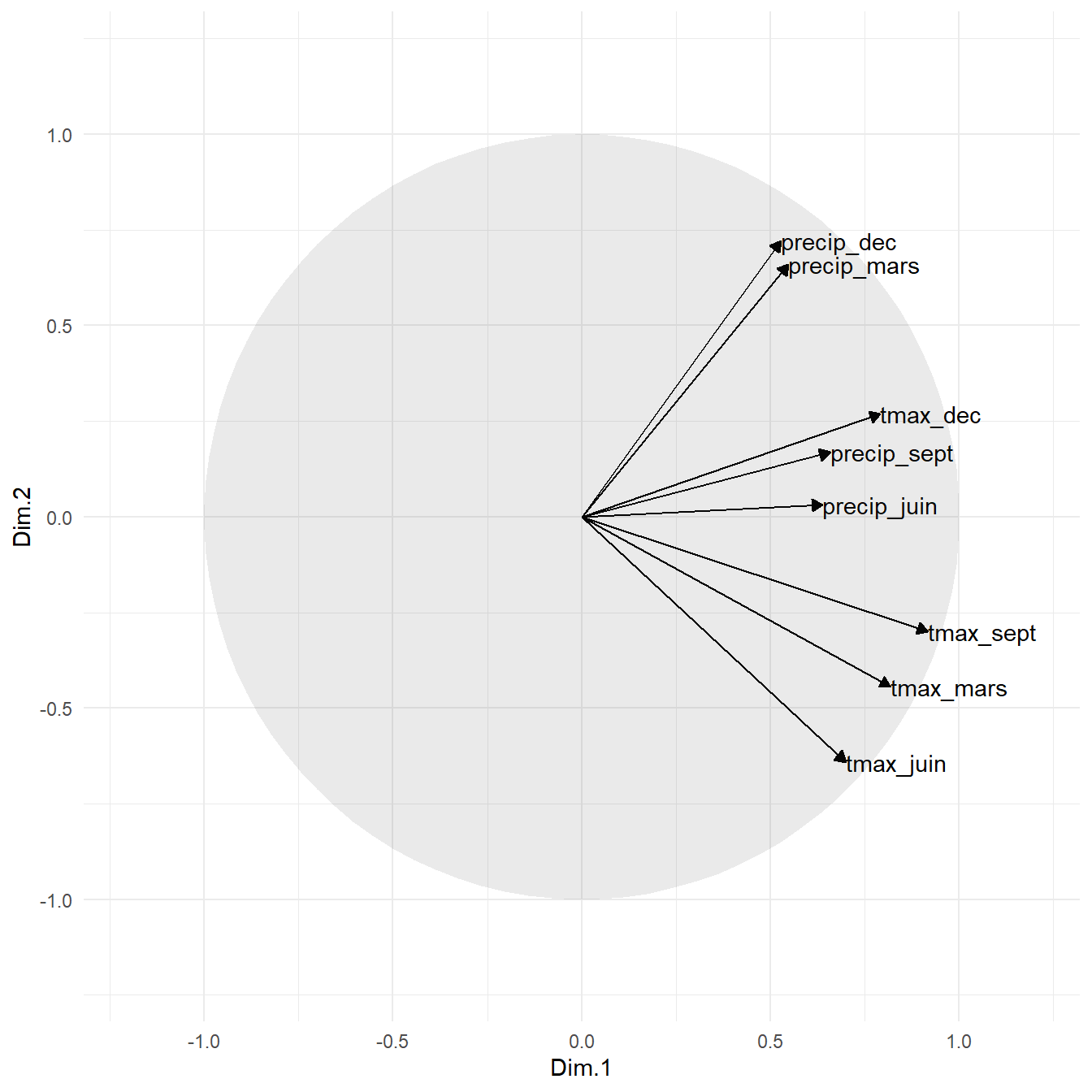

Figure 3.6: Représentation des variables sur les premiers axes de l’ACP

3.3.4.2 Contribution de chaque variable aux composantes

Nous avons vu précédemment que chaque individu contribue à la variabilité de chaque composante principale. Il en est de même pour les variables. On peut mesurer la contribution de la variable \(j\) à la composante \(k\) de la façon suivante:

\[ C^{(var)}_{j,k} = \frac{r_{j,k}^2}{\lambda_k}\]

où \(r_{j,k}\) est la coordonnée de la variable \(j\) sur l’axe factoriel \(k\).

Voici un exemple de calcul pour la première variable:

# Calculer la contribution de la première variable sur le premier axe
contribj1 <- climat_pca$var$coord[1,1]^2/climat_pca$eig[1,1]*100
contribj1

FALSE [1] 16.56336

Ceci signifie que la première variable contribue pour 16.56 % de la variance de la première composante principale. Cette mesure est très utile dans l’interprétation des axes.

On trouve aussi cette valeur dans la sortie de PCA:

# Afficher la contribution des trois premières variables sur les 3 premiers axes
climat_pca$var$contrib[1:3,1:3]

FALSE              Dim.1     Dim.2     Dim.3
FALSE tmax_mars 16.56336 11.217738 1.5128611
FALSE tmax_juin 12.08505 23.405572 0.7869995
FALSE tmax_sept 20.77615  5.138036 0.7939559

3.3.4.3 Qualité de la représentation d’une variable sur chaque composante

La qualité de la représentation d’une variable sur une composante principale correspond à la proportion de sa variabilité expliquée par la composante. Pour obtenir cette mesure, il suffit de mettre la corrélation \(r_{j,k}\) entre la variable et la composante principale au carré. Ainsi

\[Q^{(var)}_{j,k} = r^2_{j,k}\]

On trouve aussi cette valeur dans la sortie de PCA:

# Qualité des trois premiers individus sur les deux premiers axes
climat_pca$var$cos2[1:3, 1:2]

FALSE               Dim.1      Dim.2
FALSE tmax_mars 0.6701371 0.19724921
FALSE tmax_juin 0.4889488 0.41155630
FALSE tmax_sept 0.8405821 0.09034563

3.3.5 Ajout de variables et d’individus

Avec la fonction PCA, il est possible d’ajouter des variables qui ne serviront pas à calculer les composantes, mais qui pourront aider à leur interprétation. Dans l’exemple avec les variables climatiques, nous aurions par exemple pu ajouter la province comme variable qualitative (catégorielle) supplémentaire et la latitude et la longitude comme variable quantitative supplémentaire.

# Faire l'ACP en ajoutant des variables supplémentaires
climat_pca <- PCA(climat[3:13], 
                  quanti.sup = c(1,2), # Il faut mettre l'indice des variables supplémentaires
                  quali.sup = c(3),
                  ncp = 8,
                  graph = FALSE) # Vous pouvez mettre cet argument à TRUE pour voir le graphique par défaut

# Coordonnées des deux premières modalités des variables qualitatives supplémentaires 
# sur les trois premiers axes
climat_pca$quali.sup$coord[1:2, 1:3]

FALSE                        Dim.1      Dim.2      Dim.3
FALSE ALBERTA          -1.81979847 -1.2834009  0.2546469
FALSE BRITISH COLUMBIA  0.07685429  0.5285455 -0.4766487

# Coordonnées des variables quantitatives supplémentaires
climat_pca$quanti.sup$coord

FALSE                  Dim.1      Dim.2      Dim.3       Dim.4     Dim.5
FALSE latitude    -0.9174976  0.2399644 0.02139105 -0.04229497 0.1531826
FALSE elevation_m -0.1639699 -0.3280048 0.06887484 -0.03009676 0.1380872
FALSE                  Dim.6        Dim.7       Dim.8
FALSE latitude    0.03042093 -0.003214823 0.070138530
FALSE elevation_m 0.06864153  0.553118118 0.001835348

Les modalités des variables qualitative supplémentaires seront présentées dans le même graphique que les observations (g_ind). La visualisation des provinces avec les observations sur la figure 3.7 permet, notamment de remettre en question le regroupement des trois territoires (Nunavut, Territoires du Nord-Ouest et Yukon).

# Ajouter les variables qualitatives supplémentaires sur le graphique des individus
g_var_qual_sup <- g_ind +
  geom_text(data = as.data.frame(climat_pca$quali.sup$coord), 
            aes(Dim.1, Dim.2, label = rownames(climat_pca$quali.sup$coord)))

#Présenter le graphique interactif
ggplotly(g_var_qual_sup, tooltip = 'location')

Figure 3.7: Illustration d’une variable supplémentaire qualitative (la province)

Les variables quantitatives s’illustrent quant à elles sur le graphique des variables.

# mettre les coordonnées dans un dataframe
coord_quanti_sup <- as.data.frame(climat_pca$quanti.sup$coord)

# Ajouter les variables quantitatives supplémentaires sur le graphique des variables
# qui ont servi à construire l'ACP
g_var +
  geom_text(data = coord_quanti_sup, 
            aes(x = Dim.1, y = Dim.2, label = rownames(coord_quanti_sup), 
                color = 'Variables supplémentaires'),  
            hjust = 'right', 
            vjust = 'middle') + 
  geom_segment(data = coord_quanti_sup, 
               aes(x = 0, y = 0, xend = Dim.1, yend = Dim.2, 
                   color = 'Variables supplémentaires'),  
               arrow = arrow(length = unit(0.2,"cm"), type = 'closed')
               ) +
  theme(legend.position="none")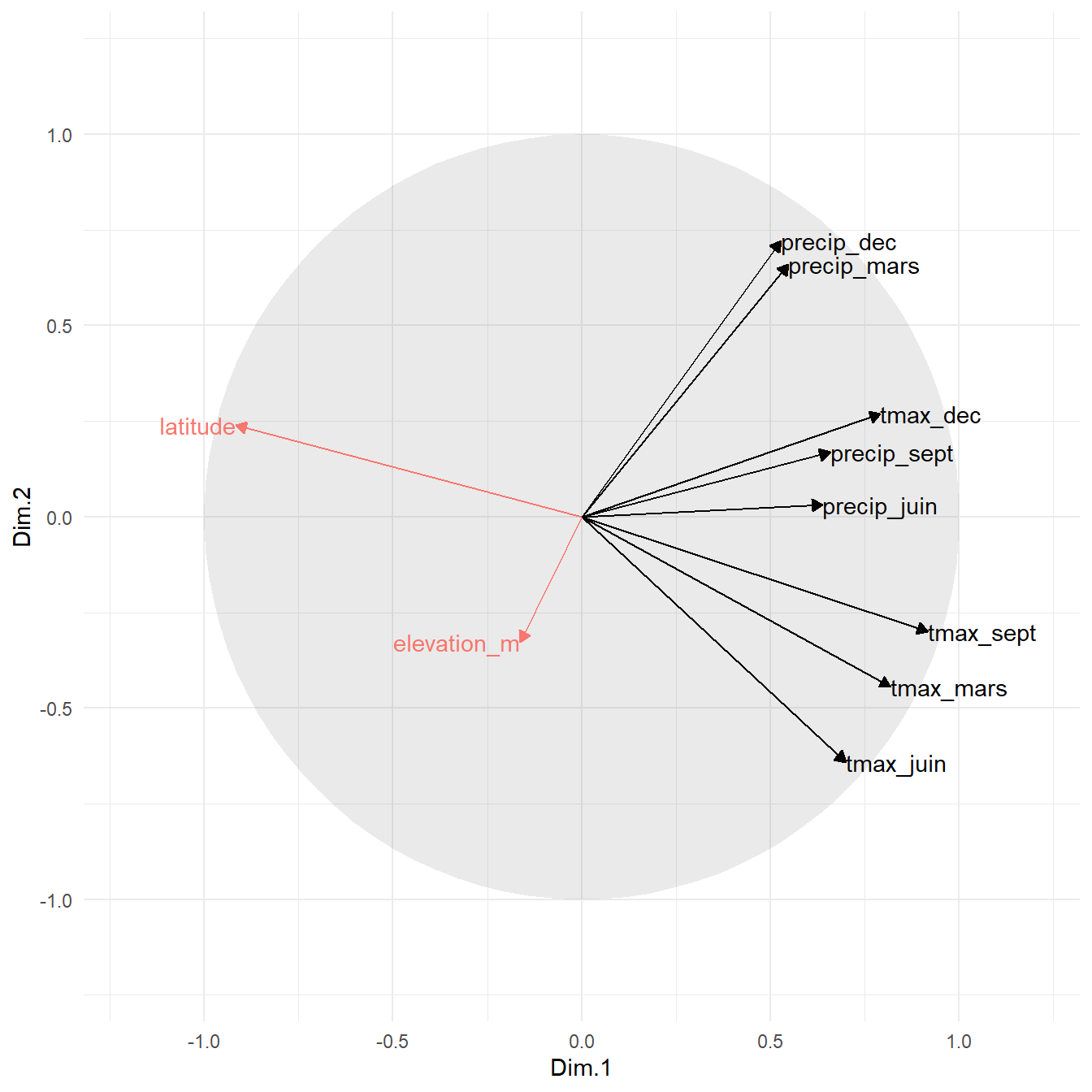

Figure 3.8: Représentation des variables et des variables supplémentaires (en rouge) sur les premiers axes de l’ACP

La figure 3.8 permet de constater que la latitude est fortement corrélée (négativement) au premier axe. Nous avions fait ce constat à partir de la figure 3.2. On constate aussi que l’élévation est peu corrélée aux deux premiers axes. De la même façon que nous l’avons fait à la section 3.3.4.3, on pourrait calculer la proportion de la variabilité dans l’altitude et l’élévation expliquée par les composante principales. On obtient facilement cette valeur avec la sortie de PCA:

# Obtenir la qualité de la représentation des variables quantitatives
# sur les dimensions de l'ACP
climat_pca$quanti.sup$cos2

FALSE                  Dim.1     Dim.2        Dim.3        Dim.4      Dim.5
FALSE latitude    0.84180182 0.0575829 0.0004575769 0.0017888643 0.02346492
FALSE elevation_m 0.02688614 0.1075871 0.0047437437 0.0009058152 0.01906807
FALSE                    Dim.6        Dim.7        Dim.8
FALSE latitude    0.0009254328 1.033509e-05 4.919413e-03
FALSE elevation_m 0.0047116592 3.059397e-01 3.368502e-06

La première dimension explique à elle seule 84.18 % de la variabilité dans la latitude alors qu’au total, l’ensemble des huit dimensions n’expliquent que 46.98 % de la variabilité sans l’altitude. La dimension la plus fortement reliée à l’altitude arrive seulement au septième rang sur huit. On peut en déduire que l’altitude n’est pas nécessairement un élément important pour expliquer la variabilité des indices climatiques choisis pour des stations étudiées. Peut-on en conclure que l’altitude n’influence pas la température et les précipitations? Absolument pas, car rappelons que les données sont de nature observationnelle (voir 2.2).

3.3.6 Variation expliquée et choix des composantes

Jusqu’à maintenant, nous nous sommes intéressés aux deux premières composantes, mais ce ne sont peut-être pas les seules composantes intéressantes à interpréter. La troisième pourrait l’être aussi. Peut-être même la quatrième et la cinquième. Il peut parfois être difficile de déterminer le nombre de composantes à analyser. Si le but est d’explorer les données, ce qui est le plus important dans ce choix, c’est l’utilité de l’interprétation qui en découle. Il existe néanmoins quelques règles pour s’aider. La plupart d’entre elles s’appuient sur la notion de variation expliquée.

Le calcul de la proportion de la variation expliquée a été détaillé dans les sections 3.1.5 et 3.2.5. On obtient aussi ces informations dans la sortie de PCA:

# Afficher les valeurs propres
kable(climat_pca$eig,
      caption = 'Proportion de la variation expliquée par chaque composante principale')

Tableau 3.2: Proportion de la variation expliquée par chaque composante principale

	eigenvalue	percentage of variance	cumulative percentage of variance
comp 1	4.0458995	50.5737439	50.57374
comp 2	1.7583689	21.9796110	72.55335
comp 3	0.7655493	9.5693665	82.12272
comp 4	0.6520047	8.1500582	90.27278
comp 5	0.3764913	4.7061409	94.97892
comp 6	0.2439982	3.0499777	98.02890
comp 7	0.1062365	1.3279568	99.35685
comp 8	0.0514516	0.6431451	100.00000

3.3.6.1 La règle du 80%

La première règle suggère tout simplement de garder le nombre de composantes principales nécessaires pour expliquer 80% de la variabilité globale. Le choix d’un pourcentage de variabilité globale de 80% est somme toute arbitraire.

Selon le tableau 3.2, on conserverait les trois premières composantes.

3.3.6.2 La règle de Kaiser

Si l’analyse en composantes principales est effectuée avec la matrice des corrélations, garder \(Y_k \Leftrightarrow \lambda_k \ge 1\). En général puisque la trace de la matrice de corrélation est égale à \(1+\cdots+1=p=\lambda_1+\cdots+\lambda_p\), alors la moyenne des valeurs propres est \(p/p=1\), et donc on ne conserve que les composantes associées à une valeur propre supérieure ou égale à cette moyenne.

Notez que si les variables sont standardisées, leur variance est égale à 1. Ainsi, choisir les composantes pour lesquelles \(\lambda > 1\) revient à choisir les composantes qui ont plus de variabilité que les variables originales.

Cette approche suggère une règle un peu plus générale. Peu importe la matrice avec laquelle l’ACP est effectuée, garder \(Y_k \Leftrightarrow \lambda_k \ge {\bar \lambda}\), où \({\bar \lambda} = (\lambda_1 + \cdots + \lambda_p)/p\).

Selon le tableau 3.2, on conserverait les deux premières composantes.

3.3.6.3 La règle de Joliffe

La règle de Joliffe est un peu plus conservatrice, dans le sens où elle est plus réticente à laisser des composantes. Si l’ACP est effectuée avec la matrice des corrélations, cette règle dit de garder \(Y_k \Leftrightarrow \lambda_k \ge 0.7\).

Selon le tableau 3.2, on conserverait les trois premières composantes.

3.3.6.4 La règle de Cattell

Cette règle est plus pragmatique, dans le sens où elle nous demande de faire le graphique des paires \((k, \lambda_k)\) (parfois appelé scree plot) et ensuite de ne garder que les \(\lambda_k\) qui précèdent le pied de l’éboulis. La justification ici est que tant que \(\lambda_k\) décroit, ajouter une composante explique de la variabilité, mais quand cette décroissance cesse, alors l’ajout de composantes additionnelles n’est pas très utile.

# Mettre les valeurs propres dans un dataframe
valeurs_propres <- as.data.frame(climat_pca$eig)

# Visualiser les valeurs propres dans un graphique d'éboulis
ggplot(data = valeurs_propres) +
  geom_point(aes(x = rownames(valeurs_propres), eigenvalue)) +
  xlab('') +
  ylab('Valeurs propres')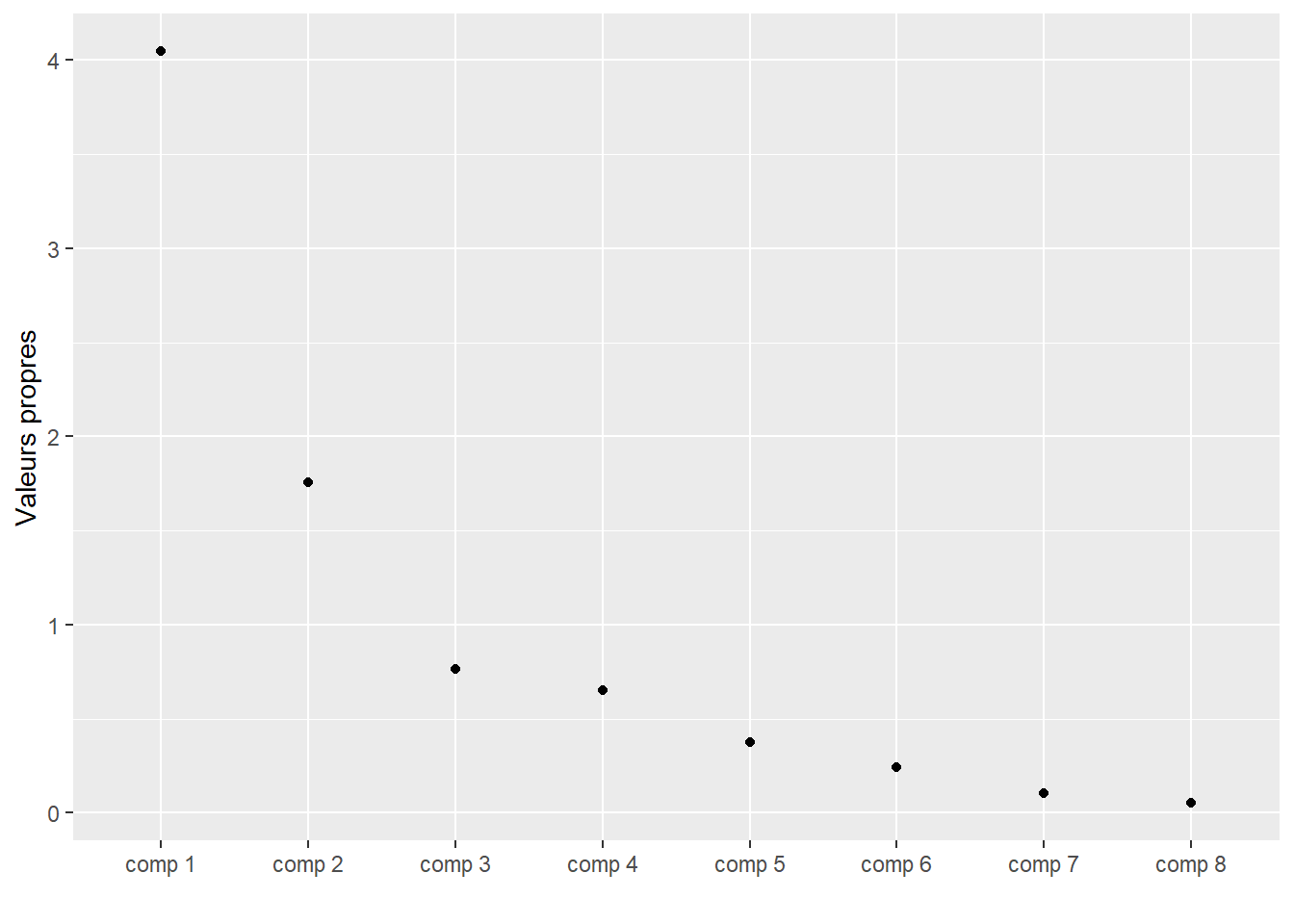 

Figure 3.9: Graphique des éboulis pour le choix du nombre de composantes à conserver

Selon la figure 3.9, on conserverait les deux premières composantes.

3.3.6.5 La règle de Horn

Si on croit que les \({\bf X}_i\) pourraient provenir d’une loi normale multidimensionnelle, alors on va

1. simuler une matrice des corrélations sur la base de \(n\) observations de la loi \({N}_p ({\bf 0}, {\bf I}_p)\);
2. extraire les valeurs propres \(\lambda_{11}, \ldots , \lambda_{1p}\);
3. répéter les deux étapes précédentes à \(K\) reprises pour obtenir \(K\) ensembles de valeurs propres \(\lambda_{k1}, \ldots , \lambda_{kp}\) pour \(1 \le k\le K\);
4. calculer \({\bar \lambda}_i = \frac{1}{K} \; \sum_{k=1}^K \lambda_{ki}, \ 1 \le i\le p\);
5. garder \(Y_k \Leftrightarrow \lambda_k \ge {\bar \lambda}_k\).

Puisque \({\bf I}_p\) a pour valeurs propres \(\alpha_1 = \cdots = \alpha_p = 1\), on s’attend à ce que \({\bar \lambda}_i > 1\) pour environ \(p/2\) valeurs. Cette méthode devrait donc garder les \(\lambda_i>1\).

3.4 Suppléments

3.4.1 Si \(p\) est très, très grand?

Les matrices \({\bf S}^2\) ou \(\hat{\mathbf{R}}=n^{-1}{\bf X}^*{\bf X}^{*\top}\) sont de dimension \(p\times p\). Si \(p\le n\), alors ces matrices seront de rang (au plus) \(p\) avec (au plus) \(p\) valeurs propres positives. Mais dans plusieurs champs d’applications, \(p>>n\) (fat data), comme par exemple en génétique ou en text mining, où \(p\) peut facilement excéder 10~000. Dans ces cas, nous sommes aux prises avec deux problèmes:

1. les matrices de variance et de corrélation auront \(n\) valeurs propres positives et un très grand nombre \(p-n\) de valeurs propres égales à 0 dont nous n’avons pas vraiment besoin;
2. mais le problème majeur sera de stocker une matrice \(p\times p\) en mémoire et demander à notre pauvre ordinateur d’en calculer les valeurs et vecteurs propres!

La solution est d’utiliser la décomposition en valeurs singulières. En effet, on va passer par \({\bf X}^{*\top}{\bf X^*}\) (qui est de dimension \(n\times n <<p\times p\)) pour aller chercher les (au plus \(n\)) valeurs propres non nulles de \(n^{-1}{\bf X^*}{\bf X}^{*\top}\) et les vecteurs propres qui lui sont associés. Du théorème A.4 on a

\[\begin{align*} n^{-1}{\bf X}^{*\top}{\bf X^*} &= n^{-1}(\mathbf{U}\mathbf{D}\mathbf{V}^\top)^\top(\mathbf{U}\mathbf{D}\mathbf{V}^\top)\\ &=n^{-1}\mathbf{V}\mathbf{D}\mathbf{U}^\top\mathbf{U}\mathbf{D}\mathbf{V}^\top=\mathbf{V}(n^{-1}\mathbf{D}^2)\mathbf{V}^\top \end{align*}\] et similairement \[\begin{align*} n^{-1}{\bf X}^{*}{\bf X}^{*\top} &= n^{-1}(\mathbf{U}\mathbf{D}\mathbf{V}^\top)(\mathbf{U}\mathbf{D}\mathbf{V}^\top)^\top\\ &=n^{-1}\mathbf{U}\mathbf{D}\mathbf{V}^\top\mathbf{V}\mathbf{D}\mathbf{U}^\top=\mathbf{U}(n^{-1}\mathbf{D}^2)\mathbf{U}^\top, \end{align*}\]

Les \(n\) premières valeurs propres que nous cherchons sont \(n^{-1}\) fois les carrés des valeurs singulières formant la matrice diagonale \(\mathbf{D}\) de la décomposition en valeurs singulières de \({\bf X}^*\) et les vecteurs propres associés sont les colonnes de la matrice \(\mathbf{U}\) de cette décomposition; les \(p-n\) valeurs propres restantes sont égales à zéro et n’expliquent donc aucune variabilité.

En pratique dans les cas où \(p\) est de grande valeur, on effectue une décomposition en valeurs singulières de \({\bf X}^*\) en demandant au logiciel d’utiliser une matrice \(\mathbf{U}\) de dimension \(n\times r\), où \(r\) est le nombre de composantes principales désirées (valeur de votre choix de 1 à \(n\)). Les valeurs propres \(\lambda_1,\ldots,\lambda_r\) de l’ACP seront \(n^{-1}\) fois les carrés des valeurs singulières obtenues et les vecteurs propres normés correspondants seront les colonnes de la matrice \(\mathbf{U}\).

3.4.2 ACP comme une première étape dans une analyse prédictive

Dans certaines applications il arrive que l’ACP soit effectuée parce que l’on va essayer de prédire la valeur d’une variable \(V\) à partir des valeurs de variables \(X_1,\ldots,X_p\) mais que \(p\) est tout simplement trop grand. Dans ces cas on applique l’ACP pour obtenir les \(k<<p\) premières composantes principales \(Y_1,\ldots,Y_k\), et ce sont ces variables qui seront utilisées pour prédire \(V\).

C’est une façon raisonnable de faire dans bien des situations, puisque les composantes principales vont retenir la majeure partie de l’information contenue dans les variables originales. D’ailleurs les grands gagnants de concours Kaggle (p.ex. Walmart en 2014) ont souvent recours à cette stratégie.

Il arrive par contre parfois qu’une variable \(X_j\) à faible variabilité soit fortement associée à \(V\) et qu’elle serait très utile si le but est de prédire \(V\).Mais comme la variabilité de \(X_j\) est faible, son poids dans les composantes principales sera négligeable. Dans ce type de situation, l’ACP n’est peut-être pas idéale. Si le but de l’ACP est de réduire la dimension afin de prédire une autre variable, alors il en existe des variantes intéressantes:

• l’analyse canonique des corrélations (canonical correlation analysis, voir Kuhn and Johnson (2013))
• la méthode des moindres carrés partiels (partial least squares, voir James et al. (2014), Kuhn and Johnson (2013))
• la régression à rang réduit (reduced rank regression, voir James et al. (2014)).

3.5 Complément

3.5.1 Exemple pour la rotation des axes

Exemple 3.2 Nous illustrerons l’aspect géométrique à l’aide d’un exemple fictif dans lequel nous simulons 200 observations de deux variablea aléatoires \((X_{i1},X_{i2})\), \(i=1,\ldots,200\) issues d’une normale multidimentionnelle \(\mathcal{N}(0,\Sigma)\) avec \[\Sigma = \begin{bmatrix} 1 & 0.8 \\ 0.8 &1 \end{bmatrix}\]

# Simuler la N(0,Sigma)
X_sim <- scale(rmvnorm(200, 
        mean = c(0,0),
        sigma = matrix(c(1,0.8,0.8,1), nrow = 2, ncol = 2)
        ))
X_sim_dat <- data.frame(X1 = X_sim[,1], X2 = X_sim[,2])

# Faire l'ACP
acp_X_sim <- prcomp(X_sim_dat, center = TRUE, scale = TRUE)

La décomposition en valeurs propres de \(\boldsymbol{S}^2\) donne les vecteurs propres suivants:

acp_X_sim$rotation

FALSE           PC1        PC2
FALSE X1 -0.7071068 -0.7071068
FALSE X2 -0.7071068  0.7071068

Remarquez que princomp donne à la matrice qui contient les vecteurs propres le nom de rotation. Ceci vient du fait que la multiplication matricielle de cette matrice par \(\boldsymbol{X}\) revient à effectuer une rotation des axes. La figure 3.10 permet de visualiser cette rotation. La première composante principale est l’axe le long duquel la variabilité est la plus forte. La première composante principale, qui s’obtient par \(Y_1=\) -0.7071068 \(x^*_1+\) -0.7071068 \(x^*_2\), nous donne la coordonnée de chaque observation sur l’abscisse de la figure de gauche. C’est l’axe selon lequel la variabilité est la plus forte. La seconde composante nous donne la coordonnée sur l’axe des ordonnées. Sa variabilité est moins forte. Ainsi dans cet exemple, même si on ne connaissait que la coordonnée des points le long de la première composante principale, on ne perdrait pas beaucoup d’information.

couleurs <- c(1:200)
g1 <- ggplot(X_sim_dat, aes(X1,X2)) +
  geom_point( size = 3, colour = couleurs) +
  ylim(-3.5,3.5) +
  xlim(-4.5,4.5) +
  ggtitle('Données simulées')
  

Y_sim  <- as.data.frame(acp_X_sim$x)
g2 <- ggplot(Y_sim, aes(PC1,PC2)) +
  geom_point( size = 3, colour = couleurs) +
  ylim(-3.5,3.5) +
  xlim(-4.5,4.5) +
  ggtitle('Composantes principales')

ggplot2.multiplot(g1,g2, cols = 2)

Figure 3.10: Aspect géométrique de l’ACP

Références

Hotelling, Harold. 1933. “Analysis of a Complex of Statistical Variables into Principal Components.” Journal of Educational Psychology 24 (6): 417.

James, G., D. Witten, T. Hastie, and R. Tibshirani. 2014. An Introduction to Statistical Learning: With Applications in R. Springer Texts in Statistics. Springer New York. https://books.google.ca/books?id=at1bmAEACAAJ.

Kuhn, M., and K. Johnson. 2013. Applied Predictive Modeling. SpringerLink : Bücher. Springer New York. https://books.google.ca/books?id=xYRDAAAAQBAJ.

Lê, Sébastien, Julie Josse, and François Husson. 2008. “FactoMineR: A Package for Multivariate Analysis.” Journal of Statistical Software 25 (1): 1–18. https://doi.org/10.18637/jss.v025.i01.

Pearson, Karl. 1901. “LIII. On Lines and Planes of Closest Fit to Systems of Points in Space.” The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 2 (11): 559–72.

---

1. Le lecteur qui n’est plus familier avec la notion de multiplicateur de Lagrange trouvera un excellent rappel sur le sujet dans l’annexe du livre de Bishop (2006).↩︎