Chapitre 5 Classification non supervisée

5.1 Introduction

La classification a pour but de regrouper (partitionner, segmenter) \(n\) observations en un certain nombre de groupes ou de classes homogènes. Il existe deux principaux types de classification:

• la classification supervisée, souvent appelée simplement classification (Classification en anglais);
• la classification non supervisée, parfois appelée partitionnement, segmentation ou regroupement (Clustering en anglais).

En classification supervisée,

• on connaît déjà le nombre de groupes qui existent dans la population;
• on connaît le groupe auquel appartient chaque observation de la population;
• on veut classer les observations dans les bons groupes à partir de différentes variables.

On peut ensuite utiliser une règle de classification pour prédire les groupes auxquels appartiennent de nouvelles observations. Des exemples classiques d’applications sont:

• identifier si une transaction bancaire est frauduleuse ou pas;
• reconnaître des chiffres écrits à la main;
• identifier le type de cancer dont souffre un patient.

En contrepartie en classification non supervisée,

• on ne connaît souvent pas le nombre de groupes qui existent dans la population;
• on ne connaît pas le groupe auquel appartient chaque observation de la population;
• on veut classer les observations dans des groupes homogènes à partir de différentes variables.

Les applications typiques sont nombreuses. Par exemple:

• en biologie : l’élaboration de la taxonomie animale;
• en psychologie : la détermination des types de personnalités présents dans un groupe d’individus;
• en text mining : le partitionnement de courriels ou de textes en fonction du sujet traité;

Il existe plusieurs familles de méthodes de classification non supervisée. Les plus communes sont:

• la classification hiérarchique;
• la classification non hiérarchique, par exemple la méthode des k-moyennes (k-means);
• la classification basée sur une densité;
• la classification basée sur des modèles statistiques/probabilistes, par exemple un mélange de lois normales.

Dans ce cours, nous nous concentrerons sur la classification hiérarchique, mais nous commencerons par un survol rapide de la méthode des k-moyennes. Le lecteur intéressé à en savoir plus peut trouver beaucoup d’information sur le sujet dans le livre de Bandyopadhyay and Saha (2013), disponible en format PDF sur le site de la bibliothèque.

5.2 Distance et similarité entre deux observations

Pour regrouper des observations en groupes homogènes, il faut tout d’abord avoir une définition de ce que sont des observations similaires ou des observations différentes. Il faut donc être en mesure de quantifier la similarité ou la distance entre deux observations . Cette première étape peut parfois être la plus difficile de tout le processus de classification, mais elle est essentielle et le premier pas de toute analyse de partitionnement.

Si les observations sont constituées de \(p\) nombres réels de valeurs du même ordre de grandeur, alors la distance euclidienne entre les deux vecteurs dans \(\mathbb{R}^p\) est une mesure tout à fait raisonnable. Mais que fait-on quand les observations sont constituées de \(p\) variables binaires (oui/non, homme/femme, présent/absent, etc.), ou \(p\) variables catégorielles, des images, des textes, ou encore plus difficile, un mélange de tout cela (par exemple pour chacun des \(n\) individus on a l’âge, le revenu, le sexe, le niveau d’éducation et une description de l’emploi en un paragraphe)?

En fait plusieurs mesures ont été développées sur mesure pour leur application particulière, à force d’expérience et d’expérimentation. Dans ce cours, nous survolerons les mesures les plus classiques qui permettent de traiter une bonne proportion des problèmes standards. Nous débuterons par les mesures plus simples ou générales pour terminer avec des mesures plus complexes ou spécialisées.

5.2.1 Mesures de distance

Une mesure de distance \(d\) doit satisfaire les propriétés suivantes pour tout \(i,j,k \in \{1, \ldots , n\}\):

• \(d(i,j) \ge 0\);
• \(d(i,i) = 0\);
• \(d(i,j) = d(j,i)\);
• \(d(i,k) \le d(i,j) + d(j,k)\).

La distance \({\cal L}_q\) entre deux vecteurs dans \(\mathbb{R}^p\) est définie par \[||x_i - x_j||_q = \left( \sum_{k=1}^p \left| x_{ik}-x_{jk} \right|^q \right)^{1/q}. \] La distance euclidienne correspond au cas où \(q=2\).

Remarquez que la distance \({\cal L}_q\) n’est PAS invariante à un changement d’échelle. cette remarque a des conséquences majeures en pratique. Par exemple, considérons le jeu de données suivant:

Tableau 5.1: Exemple illustratif pour le calcul de distance

Poids en g	Taille en cm
10	7
20	2
30	10

On trouve les distances suivantes: \[d(1,2) = 11.2, \quad d(1,3) = 20.2, \quad d(2,3) = 12.8.\] Si la taille est exprimée en millimètres, on trouve les distances suivantes. \[d(1,2) = 51.0, \quad d(1,3) = 36.1, \quad d(2,3) = 80.6.\]

On peut donc se demander si le premier objet est plus près du deuxième objet ou du troisième objet!?

Cette remarque et cet exemple expliquent pourquoi dans plusieurs situations en pratique on préfère travailler avec la distance standardisée entre les variables, \[d^2 \left( x_i, x_j \right) = \sum_{k=1}^p \left(\frac{x_{ik}-\mu_k}{s_k} - \frac{x_{jk}-\mu_k}{s_k}\right)^2 = \sum_{k=1}^p \left(\frac{x_{ik} - x_{jk}}{s_k}\right)^2\, ,\] où \[\mu_k = \mbox{moyenne de la variable } k;\ \ \ s_k = \mbox{écart-type de la variable } k.\]

On trouve les distances suivantes, peu importe l’unité de mesure utilisée: \[d(1,2) = 16, \quad d(1,3) = 42, \quad d(2,3) = 26.\]

5.2.2 Indices de similarité

Un indice de similarité \(s\) entre des objets doit satisfaire les propriétés suivantes pour tout \(i,j,k \in \{1, \ldots , n\}\):

• \(0 \leq s(i,j) \leq 1\);
• \(s(i,j) = s(j,i)\);
• \(s(i,i) = 1\).

Une distance peut se transformer en similarité en posant \[s(ij) = \frac{1}{1+d(i,j)}. \] La relation inverse n’est pas vraie, en raison de l’inégalité du triangle.

On peut aussi définir la dissemblance (dissimilarity en anglais) entre deux objets, soit \[d^*(i,j) = 1-s(i,j).\]

L’indice de similarité dépend du(des) type(s) de variables utilisées dans l’analyse. Les principaux types de variables avec lesquels on doit composer sont les suivants.

5.2.3 Variables numériques

Il s’agit de variables dont la valeur numérique mesure quelque chose de quantifiable et dont la différence entre les valeurs reflète la différence entre les objets. On peut ainsi parler du revenu en dollars, de la masse, de l’âge, etc.

Pour ce type de variable, on utilise généralement la distance euclidienne standardisée.

5.2.4 Variables nominales

Les variables nominales (ou qualitative) peuvent être binaires (deux modalités) ou polytomique (plus de deux modalités). Dans les deux cas, elles peuvent être symétriques ou asymétriques.

Les variables nominales symétriques sont des variables qualitatives (donc qui ne sont ni numériques ni ordinales) dont toutes les modalités sont aussi informatives l’une que l’autre. On peut penser par exemple au sexe (homme ou femme), à laquelle de l’une de 4 sections d’un cours des étudiants appartiennent, etc.

Les variables nominales asymétriques sont des variables qualitatives dont les modalités ne contiennent pas toutes le même niveau d’information. Ceci se produit habituellement lorsque l’une des modalités est très fréquente, un peu la modalité par défaut, mais que les autres ne le sont pas. Par exemple si une variable indique si un individu est daltonien ou pas, deux individus daltoniens ont quelque chose en commun, mais deux individus non daltoniens n’ont pas nécessairement quelque chose en commun. Un autre exemple pourrait être si une transaction est frauduleuse ou pas dans une analyse où une très faible proportion des transactions sont frauduleuses.

5.2.4.1 Variables nominales binaires

Pour des vecteurs de variables binaires symétriques, on utilise la proportion d’accords (matching coefficient) dans les éléments des vecteurs. On commence par coder l’une modalité à 0 et l’autre à 1. Si on mesure \(p\) variables binaires pour chacun de deux individus \(i\) et \(j\), on compte le nombre de variables pour lesquelles ces deux individus ont la même valeur pour une même variable, soit \(m=\sum_{k=1}^p I(x_{ik}=x_{jk})\) et la similarité est définie par \(s(i,j)=m/p\). Par exemple supposons que deux individus remplissent un questionnaire de 10 questions et que la valeur 1 représente une réponse oui et une valeur 0 une réponse non.

Tableau 5.2: Exemple pour le calcul de variables binaires

Individu	Q1	Q2	Q3	Q4	Q5	Q6	Q7	Q8	Q9	Q10
i	1	0	0	0	0	1	0	0	0	0
j	1	0	0	0	0	0	1	0	0	0

Alors la similarité entre \({x}_i\) et \({x}_{j}\) ici serait \(s(i,j)=8/10=0.8\), puisqu’ils ont donné la même réponse pour 8 des 10 questions posées.

Pour des vecteurs de variables binaires asymétriques, on assigne la modalité 1 à la valeur la plus rare (ou la plus importante) et la valeur 0 à l’autre modalité. On peut ensuite utiliser l’indice de Jaccard défini par le nombre de variables pour lesquelles \(i\) et \(j\) prennent simultanément la valeur 1 sur le nombre de variables pour lesquelles au moins l’un de \(i\) ou \(j\) n’a pas la valeur 0, soit \[ J(i,j)=\frac{\sum_{k=1}^px_{ik}x_{jk}}{\sum_{k=1}^p\{1-(1-x_{ik})(1-x_{jk})\}}. \]

Dans l’exemple ci-dessus, on aurait donc \(J(i,j)=1/3=0.33\), puisque les 7 questions pour lesquelles les deux individus donnent simultanément la valeur 0 ne sont pas comptées ni au numérateur, ni au dénominateur; pour les 3 questions qui comptent (Q1, Q6 et Q7), ils sont en accord 1 fois, d’où le 1/3.

5.2.4.2 Variables nominales polytomiques

Si une variable est composée de \(M>2\) modalités, on peut la coder en utilisant \(M-1\) variables binaires. Par exemple si les réponses possibles à une question sont Oui, Non, Je ne sais pas, on pourrait coder les trois réponses possibles ainsi:

Tableau 5.3: Exemple pour le calcul de distances de variables polytomiques

Modalités	Individu.1	Individu.2
Oui	1	0
Non	0	1
Je ne sais pas	0	0

On peut ensuite calculer la similarité entre \(i\) et \(j\) en utilisant les méthodes utilisées pour les variables binaires.

Si on a \(q\) variables binaires ou polytomiques de même nature, il est d’usage de calculer la similarité séparément pour chacune des \(q\) variables et ensuite de faire la moyenne des \(q\) similarités.

Par exemple supposons que nos deux individus \(i\) et \(j\) ont répondu à deux questions pour lesquelles ils avaient trois choix: \(i\) répond b aux deux questions alors que \(j\) répond b à la première et c à la deuxième.

Suppons que les choix sont codés selon le tableau ci-dessous.

Tableau 5.4: Exemple pour le calcul de distances de deux variables polytomiques

Individu	Q1a	Q1b	Q1c	Q2a	Q2b	Q2c
i	0	1	0	0	1	0
j	0	1	0	0	0	1

Calculons les similarités pour chaque question en supposant les modalités aussi importantes les unes que les autres. On aura \(s_{Q1}(i,j)=2/2\) et \(s_{Q2}(i,j)=1/2\). En prenant la moyenne des deux similarités, on obtient \(s(i,j)=\{s_{Q1}(i,j)+s_{Q2}(i,j)\}/2=3/4\).

Maintenant, supposons que les variables correspondant à la question 1 sont symétriques et celles correspondant à la question 2 sont asymétriques. La similarité \(s_{Q1}(i,j)=2/2\) demeure inchangée puisqu’on conserva la même règle. Pour la 2e question, on prend maintenant l’indice de Jaccard et donc \(s_{Q2}(i,j)=0/1\) car Q2a ne contribue pas au calcul. On obtient donc \(s(i,j)=\{2/2+0/1\}/2=1/2\).

5.2.5 Variables ordinales

Il s’agit de variables qui ne donnent pas une quantification précise d’un phénomène, mais dont les modalités peuvent être naturellement ordonnées. On peut penser par exemple à un revenu faible, moyen ou élevé, ou à un niveau d’accord entre tout à fait en désaccord, en désaccord, pas d’avis, d’accord, tout à fait d’accord.

On assigne habituellement un score numérique à chaque modalité de la variable ordinale, ensuite on la traite comme une variable numérique.

Il n’y a pas de règle sur les scores numériques à donner, à part qu’ils doivent être positifs et refléter l’ordre des modalités. Par exemple pour une question sur le revenu, on pourrait accorder respectivement des scores de 1, 2, 3 pour des revenus faible, moyen, élevé, ou on pourrait aussi accorder 15000, 50000, 150000; c’est un exercice de jugement et il n’existe pas de règle mathématique claire.

5.2.6 Observations constituées de plusieurs types de variables

Que doit-on faire si chaque observation est constituée de variables de plusieurs types, par exemple si pour chacun des \(n\) individus nous mesurons l’âge (numérique), le sexe (nominale symétrique), s’il est porteur d’une mutation génétique rare (nominale asymétrique) et son niveau d’accord avec une certaine politique (ordinale)? Il existe quelques façons de procéder, mais la plus commune semble être de mesurer la similarité de Gower.

On doit tout d’abord recoder toute variable nominale sous forme de variables binaires et toute variable ordinale sous forme de variable numérique et supposons qu’une fois cette opération effectuée, on obtient \(p\) variables par individu. La similarité de Gower⁴ entre \(x_i\) et \(x_j\) est définie ainsi:

\[ G(i,j)=\frac{\sum_{k=1}^p w_k\gamma_k(i,j)s_k(i,j)}{\sum_{k=1}^pw_k\gamma_k(i,j)}, \]

où \(w_k\) est un poids accordé à la variable \(k\) et \(\gamma_k(i,j)\) et \(s_k(i,j)\) sont définies différemment selon le type de la variable \(k\),

• variable \(k\) numérique ou ordinale : \(\gamma_k(i,j)=1\) et \(s_k(i,j)=1-|x_{ik}-x_{jk}|/r_k\);
• variable \(k\) nominale symétrique : \(\gamma_k(i,j)=1\) et \(s_k(i,j)=I(x_{ik}=x_{jk})\);
• variable \(k\) nominale asymétrique : \(\gamma_k(i,j)=\{1-(1-x_{ik})(1-x_{jk})\}\) et \(s_k(i,j)=I(x_{ik}=x_{jk})\).

La valeur \(r_k\) dans la similarité pour les variables numériques/ordinales est l’étendue (range) de la variable \(k\).

Il est fortement recommandé de standardiser les variables numériques/ordinales au préalable. Les poids \(w_k\) permettent de moduler l’importance de chaque variable dans la mesure de similarité.

Si on poursuit avec notre exemple, supposons que nous avons recodé les réponses de nos individus \(i\) et \(j\) de sorte que la variable 1 est numérique, la variable 2 est ordinale, les variables 3 et 4 sont des indicatrices binaires correspondant à une variable symétrique et la variable 5 est une indicatrice correspondant à une variable asymétrique. Les valeurs pour les variables 1 et 2 ont été standardisées et supposons qu’elles prennent des valeurs entre -2.5 et 2.5 (donc une étendue de 5).

Tableau 5.5: Exemple pour le calcul de distances de variables de nature différentes

Individu	Q1	Q2	Q3	Q4	Q5
i	1	2	0	1	0
j	-1	1	0	0	1

Supposons que nous voulons que la question 1 soit trois fois plus importante que les autres dans la mesure de similarité; il faut lui accorder un poids \(w_1\) qui est trois fois plus élevé que \(w_2=w_3=w_4=w_5\). On peut prendre \(w_1=3\) et \(w_2=w_3=w_4=w_5=1\). On a que:

• \(\gamma_{1}(i,j)=\gamma_{2}(i,j)=\gamma_{3}(i,j)=\gamma_{4}(i,j)=1\)
• \(\gamma_5(i,j)=1-(1-x_{i5})(1-x_{j5})=1-(1-1)(1-0)=1\).

On a ensuite - \(s_1(i,j)=1-|1-(-1)|/5=3/5\) - \(s_2(i,j)=1-|2-1|/5=4/5\) - \(s_3(i,j)=1/1\) - \(s_4(i,j)=0/1\) - \(s_5(i,j)=0/1\).

(Note: Si on a \(s_k(i,j)=0/0\) pour une variable asymétrique, c’est que \(\gamma_k(i,j)\) sera 0 et donc cette variable ne contribuera pas au calcul de \(G(i,j)\).)

\[ \begin{eqnarray*} G(i,j)&=&\frac{\sum_{k=1}^5 w_k\gamma_k(i,j)s_k(i,j)}{\sum_{k=1}^5w_k\gamma_k(i,j)}\\ &=&\left(3\times1\times\frac{3}{5}+1\times1\times\frac{4}{5}+1\times1\times\frac{1}{1}+ 1\times1\times\frac{0}{1}+1\times1\times\frac{0}{1}\right)\\ &\ &\ \ \ \ \div \left(3\times1+1\times1+1\times1+1\times1+1\times1\right)\\ &=&\frac{18/5}{7}=\frac{18}{35}\approx0.514. \end{eqnarray*} \]

5.2.7 Mesures pour des applications spécifiques

5.2.7.1 Text mining

Pour le partitionnement de \(n\) documents écrits (p.ex. pages web, courriels, lettres à l’éditeur, plaintes, documents légaux, etc.), on se crée une matrice de documents par termes où chacune des lignes de la matrice correspond à un des documents et chacune des \(p\) colonnes de la matrice correspond à l’un des mots présents dans l’ensemble des documents⁵.

L’élément de la ligne \(i\), colonne \(k\) est simplement le nombre de fois (fréquence) où le \(k\)-ème mot apparait dans le \(i\)-ème document. Ces matrices sont généralement de très grandes (nombre \(p\) de colonnes élevé) matrices éparses (la vaste majorité des éléments sont des zéros). On va fréquemment remplacer les fréquences non nulles par 1 (donc l’élément en ligne \(i\), colonne \(k\) est 1 si le mot \(j\) est dans le document \(i\), 0 sinon) ou remplacer les fréquences par des encodages qui modifient les fréquences pour tenir compte de l’importance des mots comme tf-idf, comme l’expliquent par exemple Weiss, Indurkhya, and Zhang (2015).

Si on utilise un codage présence/absence et une mesure de similarité comme la proportion d’accords ou la similarité de Jaccard, alors on aura que pratiquement toutes les paires de documents auront une similarité nulle ou très faible. C’est pourquoi on utilise habituellement cette approche pour détecter des textes où des extraits sont recopiés (par exemple détection de plagiat).

Règle générale, une mesure qui fonctionne bien pour mesurer la similarité entre des textes est celle du cosinus. Elle est définie pour des variables binaires ou numériques ainsi:

\[ s_{cos}(i,j)=\frac{\sum_{k=1}^pw_k~x_{ik}{x_{jk}}} {\sqrt{\sum_{k=1}^pw_kx_{ik}^2~\sum_{k=1}^pw_kx_{jk}^2}}. \]

Les exemples de calcul de similarité entre des documents sont très nombreux sur internet, et une bonne proportion de ces calculs utilisent la similarité du cosinus.

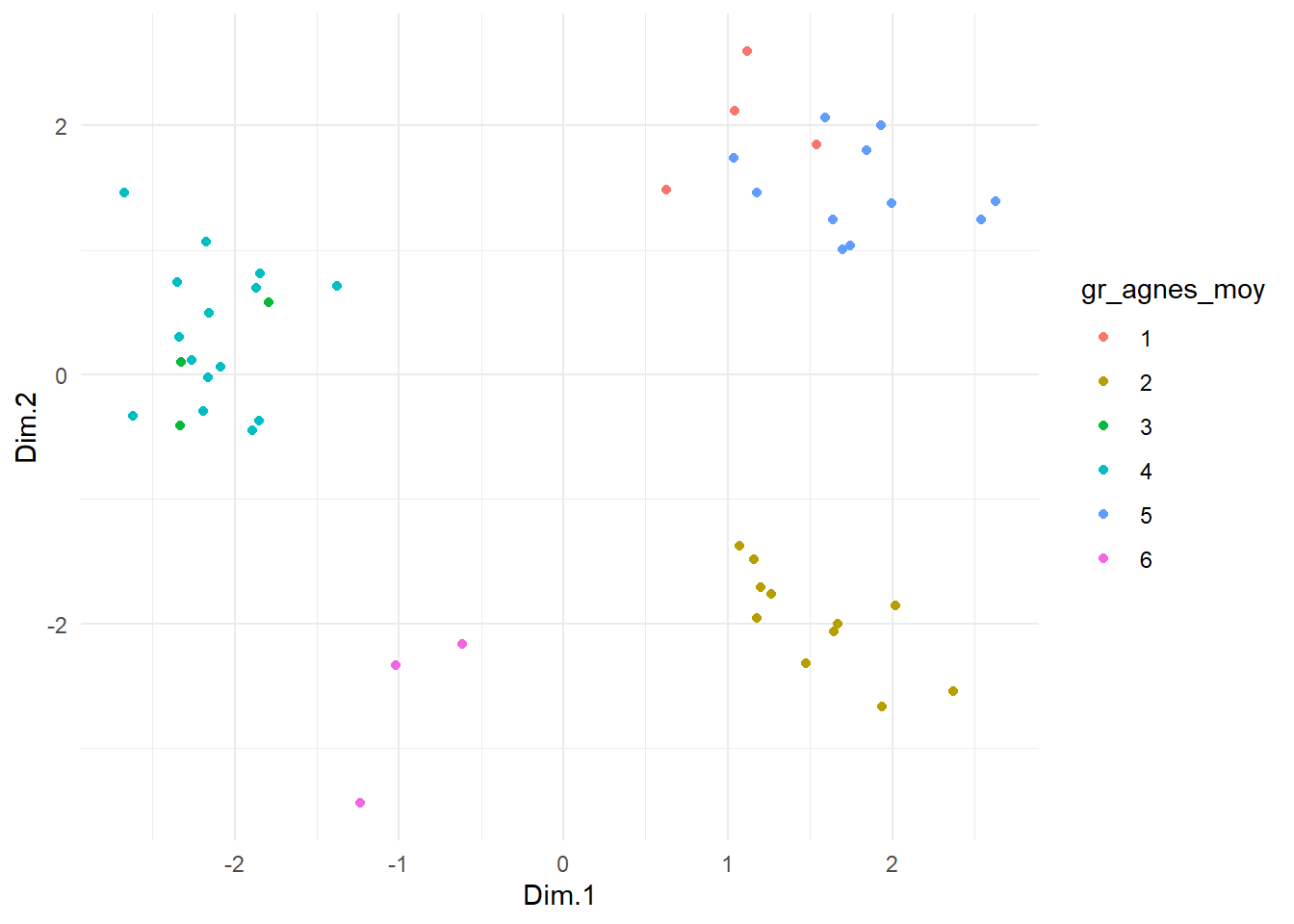
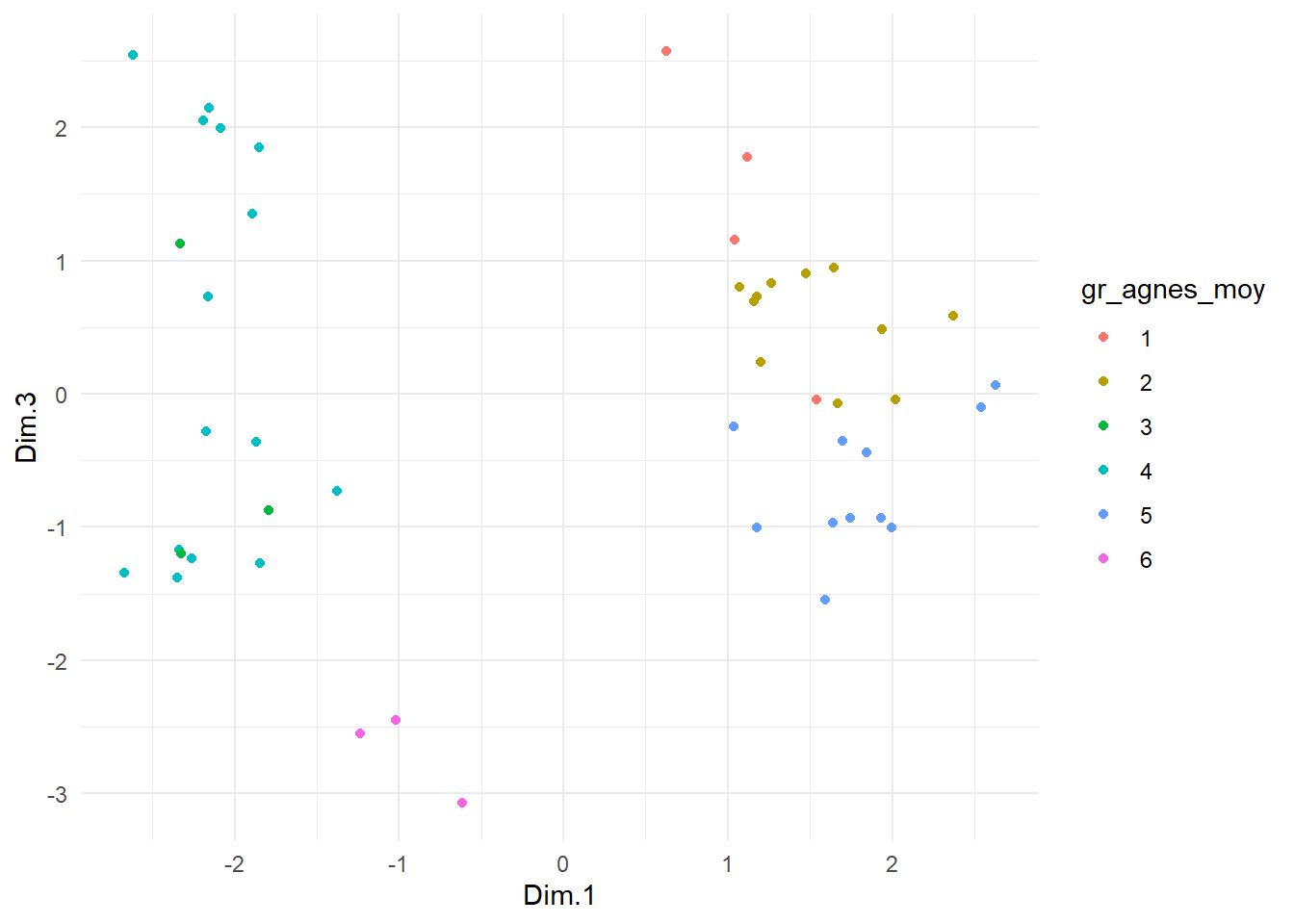
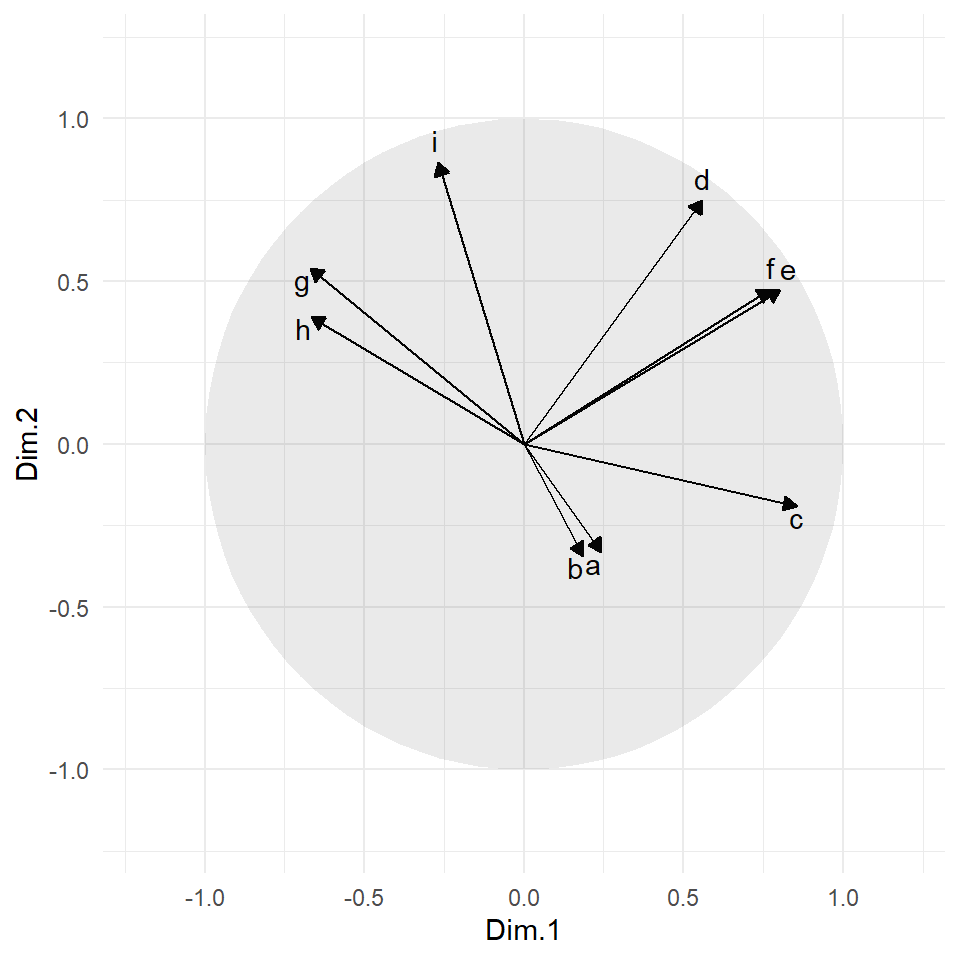
5.3 Utilisation des méthodes factorielles

Les techniques de réduction de la dimension vues aux chapitres précédents peuvent aussi être utilisées pour simplifier le calcul des similarités/distances entre les observations. Par exemple si on a \(p\) variables numériques/ordinales et que \(p\) est une très grande valeur, on peut utiliser l’analyse en composantes principales pour calculer les scores de chaque observation dans les \(k<<p\) axes principaux. On utilise ensuite ces \(k\) scores et la distance euclidienne pour calculer la distance entre les objets. Si on a plutôt \(Q\) réponses à un questionnaire à choix multiples (ou plus généralement la valeur de \(Q\) variables catégorielles), on peut calculer les scores de chaque observation dans les \(k\) premiers axes principaux d’une analyse des correspondances multiples, ensuite encore une fois utiliser ces \(k\) scores et la distance euclidienne pour calculer les distances.

Remarque : Cette stratégie est utilisée dans de nombreuses situations en pratique, en particulier quand \(p\) est très grand, et fonctionne généralement bien. Mais dans certaines situations il n’est pas impossible que des groupes nettement séparés en dimension \(p\) soient difficilement distinguables en dimension \(k<p\).

5.3.1 Mathématiquement

On veut partitionner les \(n\) observations en \(K\) groupes de façon à ce que

• les observations à l’intérieur d’un groupe soient le plus similaires possible
• les observations de deux groupes différents soient le moins similaires possible

\[C:\{1,\ldots,n\}\to \{1,\ldots,K\}\]

\[i\mapsto C(i)\]

On cherche \(C\) qui va minimiser la fonction objectif \[ W(C)=\sum_{k=1}^K\sum_{i:C(i)=k}\sum_{j:C(j)=k}d^*(x_i,x_j), \]

où \(d^*(x_i,x_j)\) est la dissimilarité entre les observations \(i\) et \(j\).

On peut démontrer que la règle qui minimise la dissimilarité \(W(C)\) à l’intérieur des classes est aussi la règle qui maximise la dissimilarité entre les observations de classes différentes.

Une première approche brute pourrait être d’essayer toutes les assignations possibles des \(n\) observations à \(K\) groupes et de voir laquelle de ces assignations donne la valeur la plus faible pour \(W(C)\). Malheureusement, il y a

\[\frac{1}{K!}\sum_{k=1}^K(-1)^{K-k} \left( \begin{array}{c} K \\ k \end{array} \right) ^n \]

possibilités ici, ce qui est une valeur beaucoup trop élevée pour que cette stratégie soit applicable en pratique. Hastie, Tibshirani, and Friedman (2009) donnent comme exemple le cas d’un tout petit échantillon de taille \(n=19\) que l’on voudrait diviser en \(K=4\) groupes, ce qui donne approximativement \(10^{10}\) possibilités! Les algorithmes que nous verrons seront donc des algorithmes dits gloutons, c’est-à-dire qu’ils vont nous donner une règle \(C\) qui minimise \(W(C)\) sur un espace restreint et qui ne nous garantissent pas que nous avons bien trouvé le \(C\) qui minimise globalement \(W(C)\).

5.4 Partitionnement

5.4.1 L’algorithme des k-moyennes

La méthode des k-moyennes s’applique à des situations où les \(p\) variables sont numériques/ordinales (et habituellement standardisées). L’objectif de la méthode est de partitionner les données en \(K\) groupes et la valeur de \(K\) est fixée . L’algorithme est relativement simple et on peut démontrer qu’à chaque étape de son exécution, la valeur de \(W(C)\) est diminuée.

1. On choisit le nombre de groupes \(K\) que l’on désire obtenir.

2. On partitionne aléatoirement les \(n\) observations en \(K\) groupes.⁶

3. On calcule les coordonnées des centroïdes (le vecteur-moyenne) pour chacun des \(K\) groupes, soit \[\mu_k = \frac{1}{N_k}\sum_{i:C(i)=k}x_i, k=1,\ldots,K,\] où \(N_k\) est le nombre d’observations dans le groupe \(k\).

4. On calcule la distance entre chaque observation et chacun des \(K\) vecteurs-moyennes.

5. On assigne chacune des \(n\) observations au groupe dont le vecteur-moyenne est le plus près.

6. On répète les étapes 3 à 5 jusqu’à ce qu’aucune observation ne soit réassignée à un nouveau groupe.

Il existe quelques variantes de cet algorithme, dont l’algorithme des K-médoides. Un médoide est un représentant d’une classe choisit comme étant l’objet le plus central de la classe. Ainsi à l’étape 4, l’algorithme des k-médoides calcule la distance entre chaque observation et chacun des \(K\) médoides. Cet algorithme est réputé plus robuste que l’algorithme des k-moyennes.

5.4.2 Exemple avec l’algorithme des k-moyennes

Supposons les 5 observations des variables \(x_1\) et \(x_2\) suivantes:

\(i\)	1	2	3	4	5
\(x_{i1}\)	-1	-0.5	0	0.5	1
\(x_{i2}\)	-1	0	0.5	-0.5	1

Itération 1

1. On choisit \(K=2\).

2. On assigne les observations 1,2,5 au groupe 1. Les observations 3 et 4 sont assignées au groupe 2.

3. On calcule les centroïdes des groupes.

\[ \mu_1 = \frac{1}{3}\left\{{-1\choose -1}+{-0.5\choose 0}+{1\choose 1}\right\}={-1/6\choose 0} \]

\[ \mu_2=\frac{1}{2}\left\{{0\choose 0.5}+{0.5\choose -0.5}\right\}={1/4\choose 0}. \]

4. On calcule la distance entre chaque observation et chacun des \(K\) centroïdes.

\(i\)	1	2	3	4	5
\(d^2(i,\mu_{1})\)	1.69	0.11	0.28	0.69	2.36
\(d^2(i,\mu_{2})\)	2.56	0.56	0.31	0.31	1.57

5. On assigne chacune des \(n\) observations au groupe dont le centroïde est le plus près. Dans ce cas-ci, les observations 1,2 et 3 sont assignées au groupe 1 et les observations 4 et 5 sont assignées au groupe 2.

Itération 2

3. On calcule les centroïdes des nouveaux groupes

\[ \mu_1=\frac{1}{3}\left\{{-1\choose -1}+{-0.5\choose 0}+{0\choose 0.5}\right\}={-1/2\choose -1/6} \]

\[ \mu_2=\frac{1}{2}\left\{{0.5\choose -0.5}+{1\choose 1}\right\}={3/4\choose 1/4}. \]

4. On calcule la distance entre chaque observation et chacun des \(K\) centroïdes.

\(i\)	1	2	3	4	5
\(d^2(i,\mu_{1})\)	0.94	0.03	{0.69}	1.11	3.61
\(d^2(i,\mu_{2})\)	4.63	1.63	0.63	0.63	0.63

5. On assigne chacune des \(n\) observations au groupe dont le centroïde est le plus près. L’observation 3 passe du groupe 1 au groupe 2.

Itération 3

3. On calcule les centroïdes des nouveaux groupes

\[ \mu_1 =\frac{1}{2}\left\{{-1\choose -1}+{-0.5\choose 0}\right\}={-3/4\choose -1/2} \]

\[ \mu_2=\frac{1}{3}\left\{{0\choose 0.5}+{0.5\choose -0.5}+{1\choose 1}\right\}={1/2\choose 1/3}. \]

4. On calcule la distance entre chaque observation et chacun des \(K\) centroïdes.

\(i\)	1	2	3	4	5
\(d^2(i,\mu_{1})\)	0.31	0.31	{1.56}	1.56	5.31
\(d^2(i,\mu_{2})\)	4.03	1.11	0.28	0.69	0.69

5. On assigne chacune des \(n\) observations au groupe dont le centroïde est le plus près. Toutes les observations sont déjà dans le groupe dont le centroïde est le plus près. Il n’y a aucun changement. L’algorithme est terminé.

5.5 Classification hiérarchique

Si on ne sait pas quelle valeur de \(K\) utiliser ou si les observations ne sont pas constituées de variables numériques ou ordinales, la méthode des k-moyennes ne s’applique pas (il faut une distance en bonne et due forme pour que les assignations aux groupes via les distances à un vecteur-moyenne aient du sens). On peut alors utiliser un des nombreux algorithmes de classification hiérarchique. La classification hiérarchique permet d’obtenir des partitions tout imbriquées les unes dans les autres. Il existe deux types d’algorithmes pour effectuer de la classification hiérarchique:

• les algorithmes ascendants;
• les algorithmes descendants.

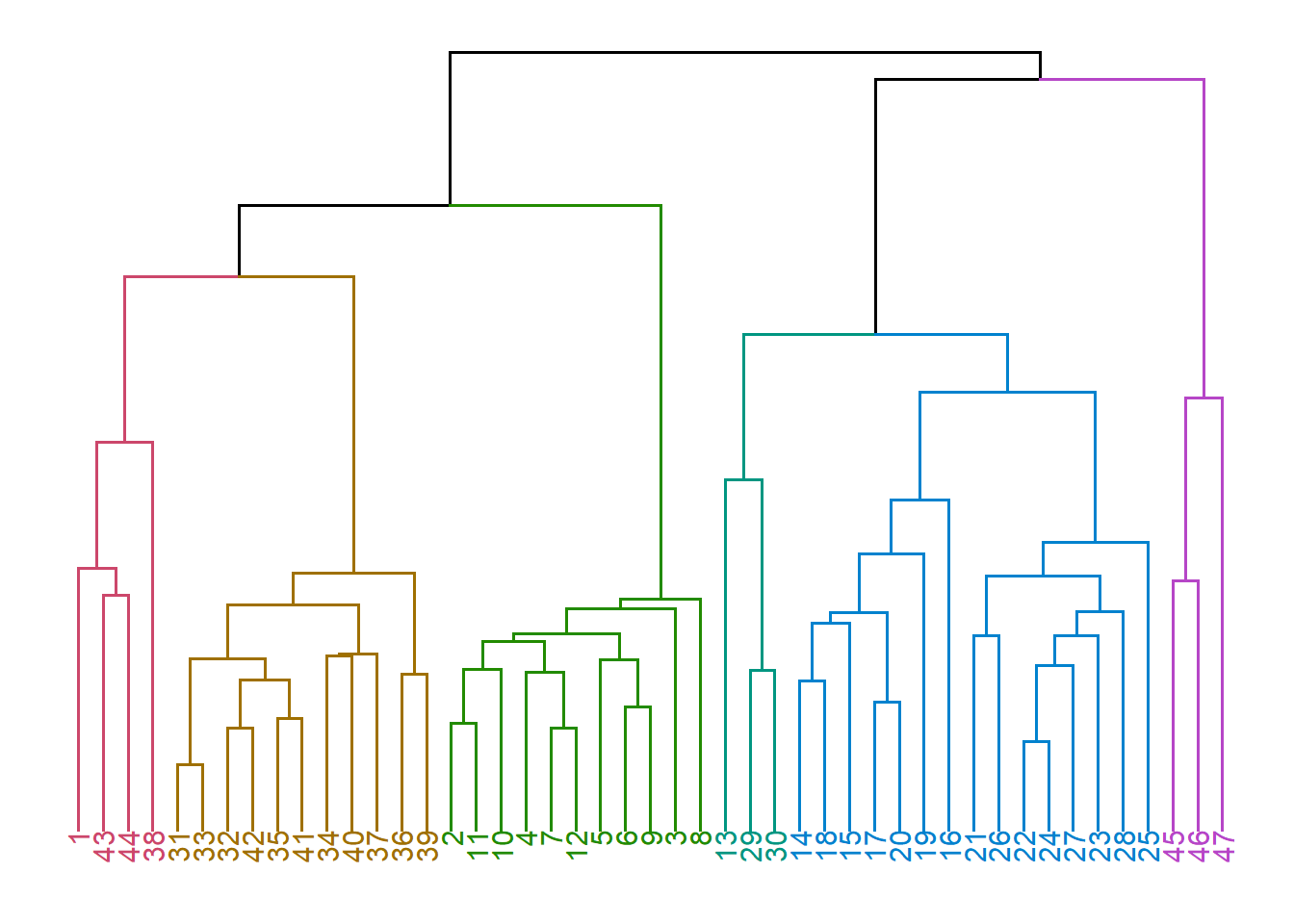
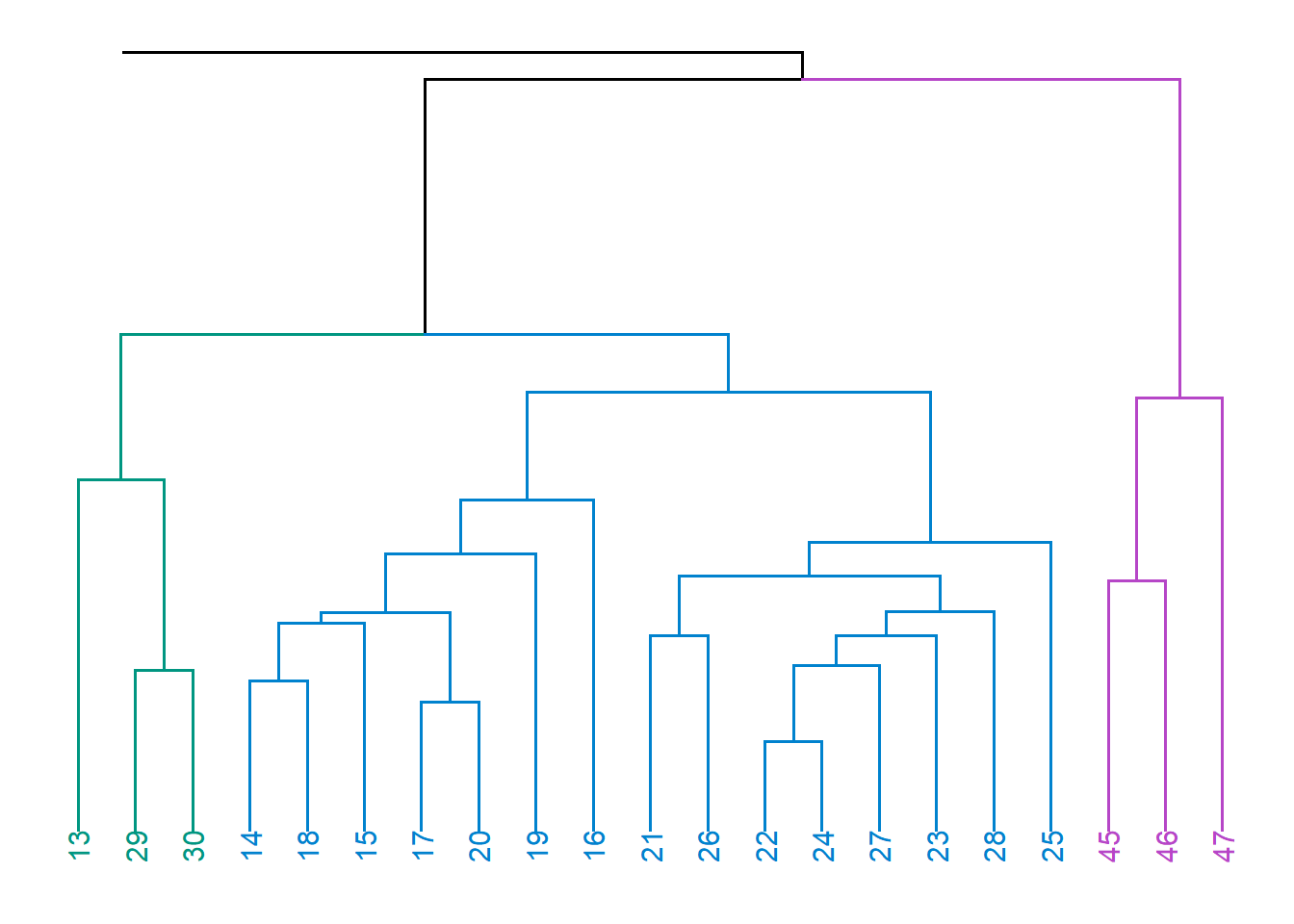
L’exécution d’un tel algorithme ne donne pas une seule partition, mais \(n\) partitions: une partition avec un groupe, une partition avec deux groupes, …, une partition avec \(n\) groupes. Nous verrons plus tard comment résumer de façon visuelle le résultat d’une classification hiérarchique à l’aide d’un graphique en forme d’arbre appelé dendogramme. Nous verrons aussi des critères qui peuvent aider à choisir l’une parmi les \(n\) partitions proposées par l’algorithme.

Un algorithme descendant fonctionne ainsi:

• au départ, toutes les observations sont dans un seul et même groupe de \(n\) observations;
• à chaque étape, on divise le groupe le moins homogène en deux groupes;
• à la fin, après \(n\) étapes, chaque observation est son propre groupe, c’est-à-dire qu’on obtient \(n\) groupes contenant une seule observation.

Un algorithme ascendant procède à l’inverse

• au départ chaque observation est son propre groupe, c’est-à-dire qu’on démarre avec \(n\) groupes contenant chacun une seule observation;
• à chaque étape, on fusionne les deux groupes les plus similaires;
• à la fin des \(n\) étapes, on obtient un seul groupe contenant toutes les \(n\) observations

Comme les algorithmes descendants demandent beaucoup de temps de calcul (ce n’est pas tout de déterminer quel groupe scinder en 2, mais on doit déterminer comment se découpage doit se faire) et qu’ils sont peu utilisés en pratique, nous nous concentrerons sur les algorithmes ascendants.

5.5.1 Algorithmes ascendants

Les implémentations de la classification hiérarchique se distinguent de deux manières:

• leur façon de mesurer les distances ou les similarités entre deux observations;
• leur façon de mesurer les distances ou les similarités entre deux groupes.

Pour mettre en oeuvre les algorithmes mentionnés précédemment, on doit définir \(d(A, B)\), la distance entre deux groupes d’observations \(A\) et \(B\) tels que

• les groupes \(A\) et \(B\) sont des sous-ensembles des observations du jeu de données;
• l’intersection entre les groupes \(A\) et \(B\) est l’ensemble vide.

Nous avons vu toutes sortes de méthodes pour calculer la distance entre une paire d’observations, mais nous devons maintenant considérer des méthodes pour calculer la distance entre une paire de groupes d’observations. Il existe plusieurs façons de calculer une telle distance entre deux groupes lors de l’exécution d’une classification hiérarchique ascendante. Nous commençons par les lister, nous présenterons ensuite les points forts et les points faibles de chacune des méthodes.

5.5.1.1 Méthode du plus proche voisin (single linkage)

La distance entre deux groupes se définit comme suit pour cette méthode: \[d\left( A, B \right) = \min \left\{ d_{ij}: i \in A, j \in B \right\} .\]

Si on travaille plutôt avec des indices de similarité, on pose \[s\left( A, B \right) = \max \left\{ s_{ij}: i \in A, j \in B \right\} .\]

On voit donc d’où la méthode tire son nom: la distance/similarité entre deux groupes d’observations est tout simplement la distance/similarité entre les points de chaque groupe qui sont les plus rapprochés/similaires.

Points forts	Points faibles
Donne de bons résultats lorsque les variables sont de types différents	Tend à former un grand groupe avec plusieurs petits groupes satellites
Possède d’excellentes propriétés théoriques	Les propriétés théoriques ne semblent pas se réaliser en pratique dans certaines études
Permet de créer des groupes dont la forme est très irrégulière	Perd de l’efficacité si les vrais groupes sont de forme régulière
Est robuste aux données aberrantes

5.5.1.2 Méthode du voisin le plus distant (complete linkage)

La distance entre deux groupes se définit comme suit pour cette méthode: \[d\left( A, B \right) = \max \left\{ d_{ij}: i \in A, j \in B \right\} .\]

Si on travaille plut^ot avec des indices de similarité, on pose \[s\left( A, B \right) = \min \left\{ s_{ij}: i \in A, j \in B \right\} .\]

Encore une fois comme le nom l’indique, la distance/similarité entre deux groupes d’observations est tout simplement la distance/similarité entre les points de chaque groupe qui sont les plus éloignés/dissimilaires.

Cette méthode est peu utilisée en pratique.

Points forts	Points faibles
Donne de bons résultats lorsque les variables sont de types différents	Est extrêmement sensible aux données aberrantes

La méthode du voisin le plus distant tend à former des groupes de tailles égales.

5.5.1.3 Méthode de la moyenne (average linkage)

La distance entre deux groupes se définit comme suit pour cette méthode: \[d \left( A, B \right) = \frac{1}{n_A n_B} \sum_{i \in A} \sum_{j \in B} d \left(x_i, x_j \right), \] où \(n_A\) est le nombre d’observations dans le groupe \(A\) et \(n_B\) est le nombre d’observations dans le groupe \(B\).

On doit donc calculer les \(n_A\times n_B\) distances possibles entre les points des deux groupes, ensuite on prend la moyenne de ces distances comme étant celle qui sépare les deux groupes.

La méthode de la moyenne forme des groupes de faible variance et de même variance.

5.5.1.4 Méthode du centroïde

La distance entre deux groupes se définit comme suit pour cette méthode: \[d \left( A, B \right) = d\left( {\bar x}_A, {\bar x}_B \right),\] où \[{\bar x}_A = \frac{1}{n_A} \, \sum_{i \in A} x_i, \quad {\bar x}_B = \frac{1}{n_B} \, \sum_{j \in B} x_j. \]

La moyenne \({\bar x}_{AB}\) du nouveau groupe résultant de la fusion des groupes \(A\) et \(B\) se calcule comme suit: \[{\bar x}_{AB} = \frac{n_A {\bar x}_A + n_B {\bar x}_B}{n_A + n_B} \,.\]

Points forts	Points faibles
Très robuste aux données aberrantes	Est peu efficace en l’absence de données aberrantes.

5.5.1.5 Méthode de la médiane

À une étape donnée, nous avons toujours à notre disposition la distance entre les groupes déjà formés. On fusionne les deux groupes les plus similaires, disons \(A\) et \(B\) pour obtenir un groupe \(AB\). Avec la méthode de la médiane, la distance entre le nouveau groupe \(AB\) et tout autre groupe \(C\) est donnée par \[d(AB,C)=\frac{d(A,C)+d(B,C)}{2}-d(A,B)/4.\]

Points forts	Points faibles
Très, très robuste en présence de données aberrantes	Est très peu efficace en l’absence de données aberrantes.

5.5.1.6 Méthode de Ward

La méthode de Ward est une variante de la méthode du centroïde pour tenir compte de la taille des groupes. Elle a été conçue de sorte à être optimale si les \(n\) vecteurs \(x_1,\ldots,x_n\) suivent des lois normales multivariées de \(K\) moyennes différentes, mais toutes de même matrice de variance-covariance.

Elle est basée sur les sommes de carrés suivantes:

\[ \begin{align} SC_A &= \sum_{i \in A} (x_i - {\bar x}_A)^\top (x_i - {\bar x}_A),\\ SC_B &= \sum_{j \in B} (x_j - {\bar x}_B)^\top (x_j - {\bar x}_B),\\ SC_{AB} &= \sum_{k \in A \cup B} (x_k - {\bar x}_{AB})^\top (x_k -{\bar x}_{AB}), \end{align} \]

où \({\bar x}_A\), \({\bar x}_B\) et \({\bar x}_{AB}\) sont calculées comme dans la méthode du centroïde.

On regroupe ensuite les classes \(A\) et \(B\) pour lesquelles

\[ \begin{align*} I_{AB} &= SC_{AB} - SC_A - SC_B \\ \\ &= \frac{n_An_B}{n_A+n_B} \, \left( {\bar x}_A - {\bar x}_B \right)^\top \left( {\bar x}_A - {\bar x}_B \right)\\ &=\frac{d^2(\bar{x}_A,\bar{x}_B)}{\frac{1}{n_A}+\frac{1}{n_B}} \end{align*} \]

est minimale.

Points forts	Points faibles
Est optimale si les observations sont approximativement distribuées selon une loi normale multidimensionnelle de même matrice de variances-covariances	Est sensible aux données aberrantes

Cette méthode tend à former des groupes de même taille

5.5.1.7 Méthode flexible (Supplément)

Les auteurs de cette méthode ont remarqué que pour plusieurs méthodes connues, on a les relations suivantes:

\[ \begin{align*} d(C, A \cup B) = & \; \alpha_A \; d(C,A) \; + \\[4pt] & \; \alpha_B \; d(C,B) \; + \\[4pt] & \; \, \beta \; d(A,B) \; + \\[4pt] & \; \, \gamma \; | d(C,A) - d(C,B)| \end{align*} \]

Méthode	\(\alpha_A\)	\(\alpha_B\)	\(\beta\)	\(\gamma\)
Plus proche	\(1/2\)	\(1/2\)	\(0\)	\(-1/2\)
Plus distant	\(1/2\)	\(1/2\)	\(0\)	\(1/2\)
Médiane	\(1/2\)	\(1/2\)	\(-1/4\)	\(0\)
Moyenne	\(\displaystyle \frac{n_A}{n_A+n_B}\)	\(\displaystyle \frac{n_B}{n_A+n_B}\)	\(0\)	\(0\)
Centroïde	\(\displaystyle \frac{n_A}{n_A+n_B}\)	\(\displaystyle \frac{n_B}{n_A+n_B}\)	\(\displaystyle -\frac{n_An_B}{n_A + n_B}\)	\(0\)
Ward	\(\displaystyle \frac{n_A+n_C}{n_A+n_B+n_C}\)	\(\displaystyle \frac{n_B+n_C}{n_A+n_B+n_C}\)	\(\displaystyle -\frac{n_C}{n_A+n_B+n_C}\)	\(0\)

Avec la méthode flexible, on impose {arbitrairement} les contraintes suivantes: \[\alpha_A + \alpha_B + \beta = 1, \quad \alpha_A = \alpha_B, \quad \gamma = 0 . \]

Ainsi, \[\alpha _ A = \alpha _ B = (1-\beta)/2\] et il ne reste qu’à choisir \(\beta\). Les auteurs suggèrent de poser, \(\beta = -0.25,\) mais ils recommandent plutôt de poser \(\beta = -0.5\) lorsque l’on soupçonne la présence de données aberrantes.

5.5.2 Exemple avec la méthode du plus proche voisin

Illustrons l’algorithme ascendant avec la méthode du plus proche voisin. Prenons l’exemple suivant avec deux variables et \(n = 5\) individus.

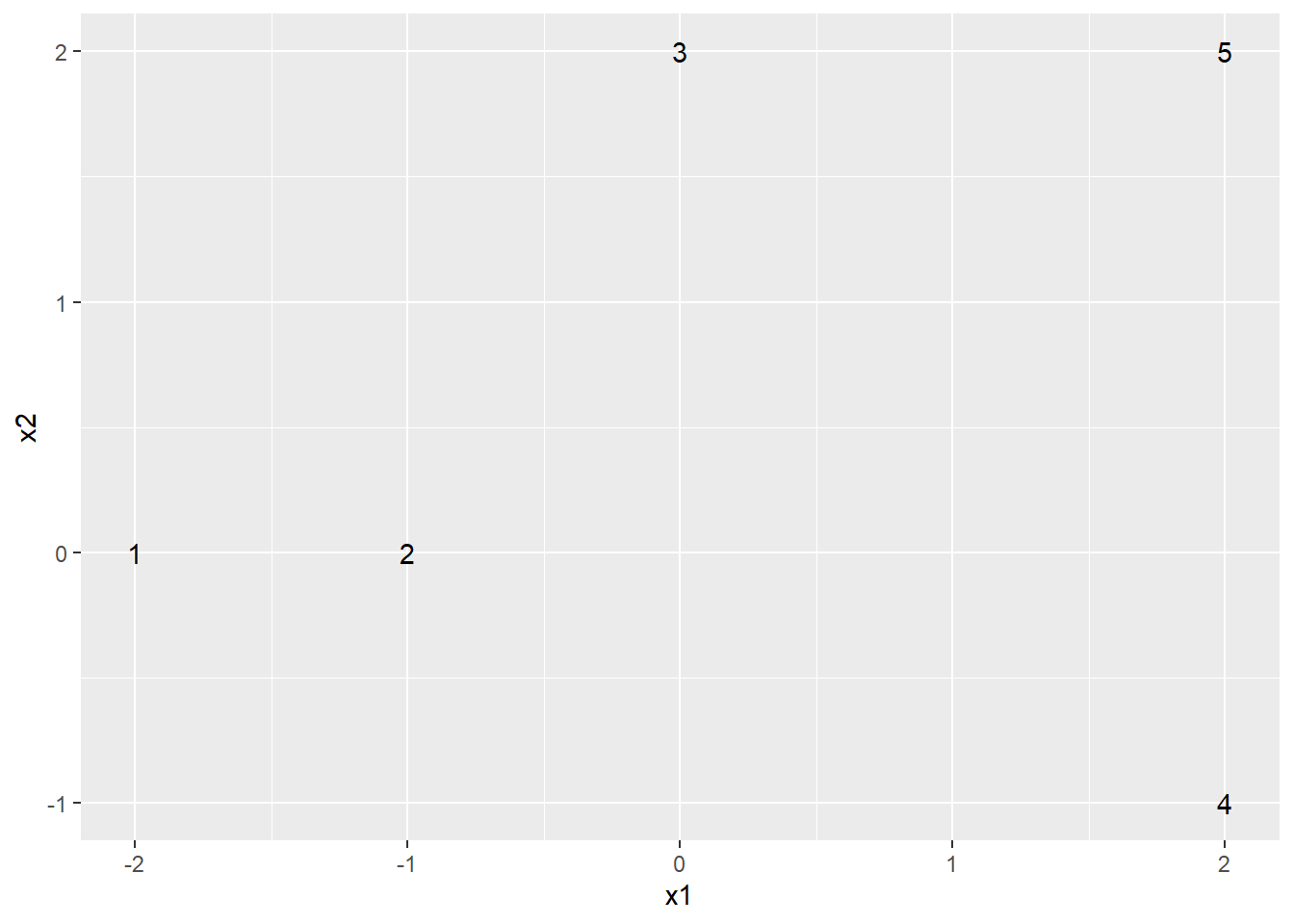
x1	x2
-2	0
-1	0
0	2
2	-1
2	2

Nous aurons aussi besoin de la matrice des distances entre chaque observation.

print(round(dist(ex_classif ),2))

FALSE      1    2    3    4
FALSE 2 1.00               
FALSE 3 2.83 2.24          
FALSE 4 4.12 3.16 3.61     
FALSE 5 4.47 3.61 2.00 3.00

Étape 1

Au départ, chacun des 5 individus est dans son propre groupe. Il s’agit de notre première partition (\(P_1\)). Elle contient \(n=5\) groupes.

\[P_1 = (\{1\},\{2\},\{3\},\{4\},\{5\})\]

Étape 2

On regarde quels individus sont les plus proches dans notre matrice de distance. Il s’agit des individus 1 et 2, dont la distance est de 1. On regroupe ces deux individus ensemble pour former un seul groupe. Nous avons maintenant notre deuxième partition. Elle contient \(n-1=4\) groupes.

\[P_2 = (\{1,2\},\{3\},\{4\},\{5\})\]

Étape 3

On poursuit en cherchant les individus les plus proches qui ne sont pas déjà dans le même groupe. Il s’agit des individus 3 et 5, dont la distance est de 2. On regroupe ces deux individus ensemble pour former un seul groupe. Nous avons maintenant notre troisième partition. Elle contient \(n-2=3\) groupes.

\[P_3 = (\{1,2\},\{3,5\},\{4\})\]

Étape 4

On poursuit, toujours en cherchant les individus les plus près qui ne sont pas déjà dans le même groupe. Il s’agit des individus 2 et 3, dont la distance est de 2.24. Puisque l’individu 2 est déjà regroupé avec l’individu 1 et que l’individu 3 est déjà groupé avec l’individu 5, il en résulte une fusion de ces deux groupes. Nous obtenons notre quatrième partition. Elle contient \(n-3 = 2\) groupes.

\[P_4 = (\{1,2,3,5\},\{4\})\]

Étape 5

On poursuit, toujours en cherchant les individus les plus près qui ne sont pas déjà dans le même groupe. Il s’agit des individus 4 et 5, dont la distance est de 3. Puisque l’individu 5 est déjà regroupé avec les individus 1,2 et 3, l’individu 4 est ajouté au groupe. Nous obtenons notre cinquième et dernière partition. Elle contient \(n-1 = 1\) groupes.

\[P_5 = (\{1,2,3,4,5\})\]

Évidemment, nous ne voulons pas un seul groupe. Il faut donc «arrêter» l’algorithme au bon endroit pour obtenir le nombre de groupes désirés. Par exemple, si on avait voulu deux groupes, il aurait fallu arrêter à l’étape 4.

5.6 Avantages et inconvénients des algorithmes ascendants et k-moyenne

La méthode des k-moyennes est rapide et donne de bons résultats pour des variables quantitatives ou ordinales. Elle a trois principaux inconvénients:

1. Elle est très sensible au choix des centroïdes initiaux.
2. En principe, elle ne peut être utilisée qu’avec des variables ordinales ou continues.
3. Il faut choisir au préalable le nombre de groupes. Cette étape peut être facile dans certains contextes (par exemple, l’application requière qu’il y ait un nombre prédéterminé de groupes), mais il est en général difficile de savoir d’avance combien de groupes seront nécessaires pour bien segmenter notre population.

La méthode hiérarchique ascendante ne nous oblige pas à connaître d’avance le nombre de groupes. Il est possible de couper l’arbre à différents endroits et de tenter d’interpréter chacune des partitions. Il existe aussi certaines mesures pour nous aider à faire ce choix. Un autre avantage de cette méthode est qu’elle permet d’utiliser différents types de variables. Les principaux inconvénients de la méthode hiérarchique ascendante sont:

1. Elle est exigeante en termes de temps de calcul
2. Une fois que deux individus sont groupés, ils ne seront jamais séparés.

En général, il sera intéressant de combiner ces deux approches. Par exemple, on peut commencer par une classification ascendante pour déterminer le nombre de groupes intéressant, puis utiliser les centroïdes de ces groupes pour initialiser l’algorithme des k-moyennes.

5.7 En pratique

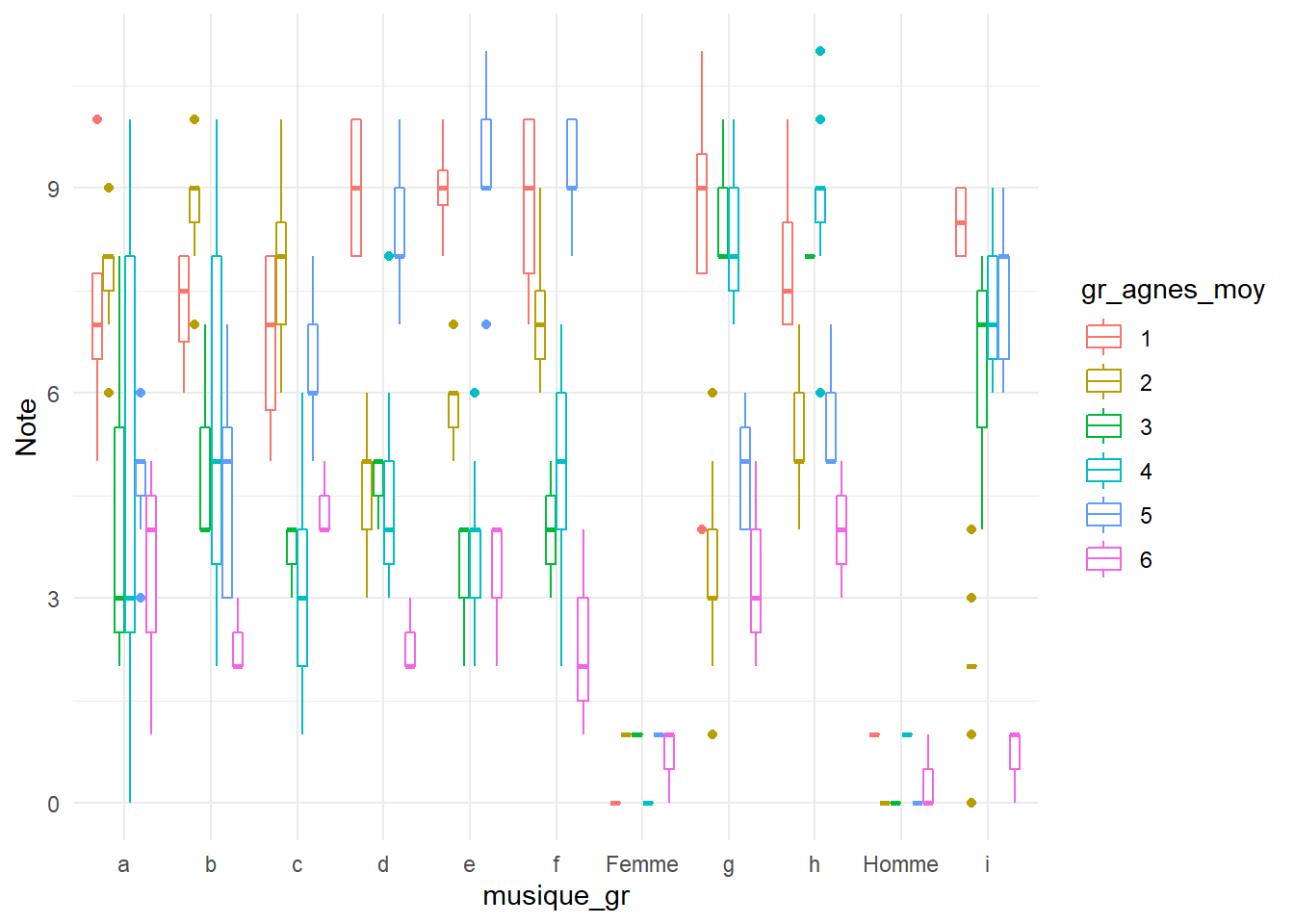
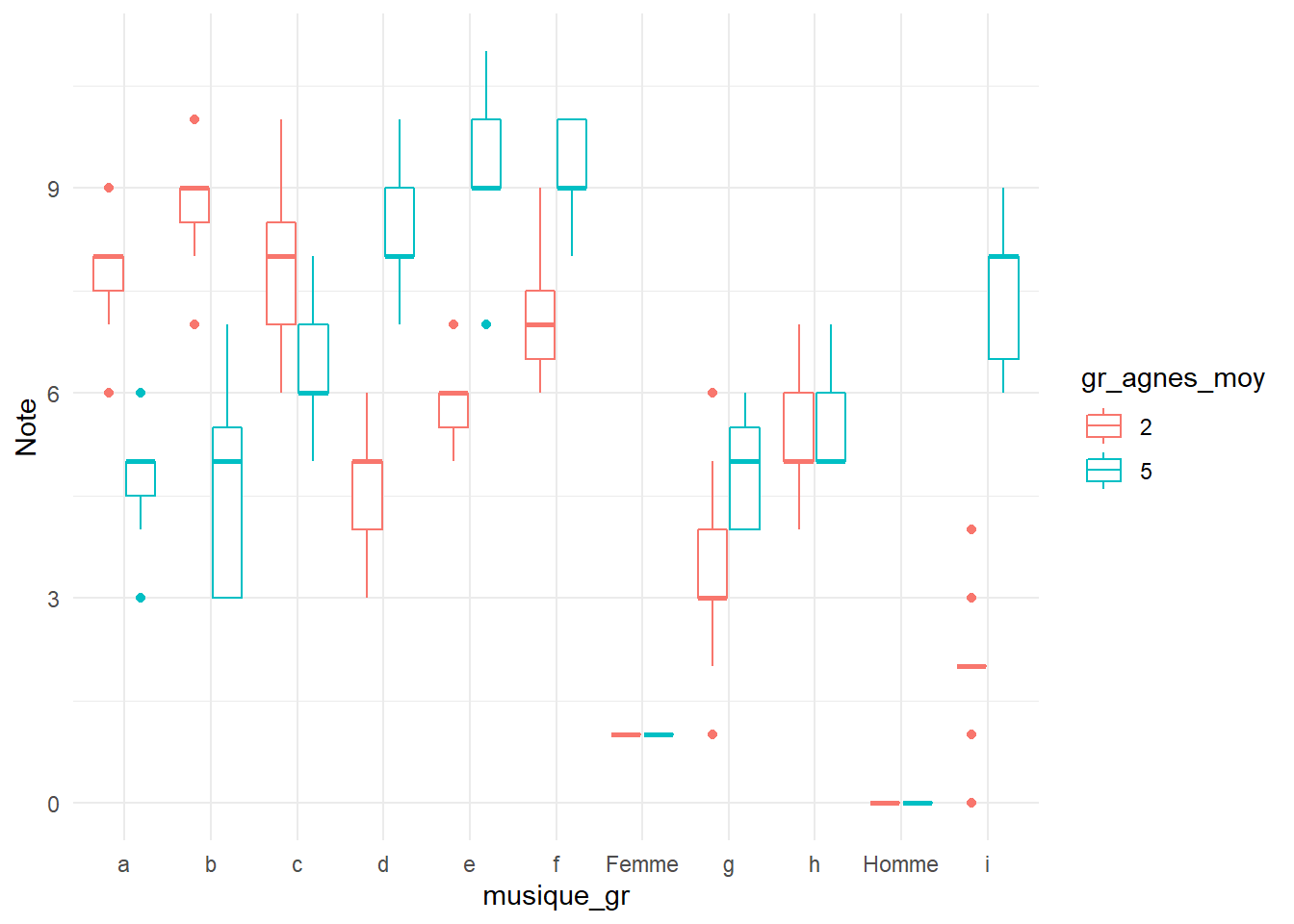
Pour illustrer les algorithmes de classification non supervisée, nous utiliserons un jeu de données simulées qui contient les préférences musicales de 47 individus. Les variables a à i donnent le score d’appréciation (sur une échelle de 1 à 10) de chaque individu pour les extraits musicaux a à i. La variable genre correspond au genre de la personne (homme ou femme).

load('don/musique.RData')

5.7.1 Librairies et fonctions

La librairie stats est une librairie de base de R. Elle contient une fonction pour effectuer la classification par l’algorithme des k-moyennes (la fonction kmeans) et une fonction pour effectuer une classification hiérarchique ascendante (la fonction hclust). Ces deux fonctions sont efficaces et offrent plusieurs options intéressantes. Malheureusement, elles ne permettent pas de traiter des variables de natures différentes (par exemple, des variables numériques et catégorielles). Or une grande partie des jeux de données utilisés en segmentation contiennent des variables de nature différentes. Pour cette raison, nous nous concentrerons sur les fonctions de la librairie cluster, plus particulièrement sur les trois fonctions suivantes: daisy, agnes et pam.

library(cluster)